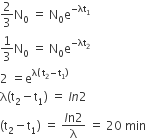Half-lives of two radioactive elements A and B are 20 minutes and 40 minutes, respectively. Initially, the samples have equal number of nuclei. After 80 minutes, the ratio of decayed numbers of A and B nuclei will be:
1: 16
4 : 1
1: 4
1: 4
D.
1: 4
Given 80 min = 4 half-lives of A = 2 half-lives of B.
Let the initial number of nuclei in each sample be N.
For radioactive element A,
NA after 80 min = N/24
⇒ Number of A nuclides decayed =
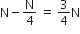
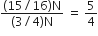
Proton, Deuteron and alpha particle of the same kinetic energy is moving in circular trajectories in a constant magnetic field. The radii of the proton, deuteron and alpha particle are respectively rp, rd and rα. Which one of the following relations is correct?
rα = rp= rd
rα = rp< rd
rα > rd> rp
rα > rd> rp
B.
rα = rp< rd
For charged particle moving with a speed v, in magnetic field B, on a circular track of radius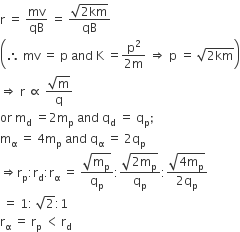
(a) Draw the plot of binding energy per nucleon (BE/A) as a function of mass number A. Write two important conclusions that can be drawn regarding the nature of nuclear force.
(b) Use this graph to explain the release of energy in both the processes of nuclear fusion and fission.
(c) Write the basic nuclear process of neutron undergoing –decay. Why is the detection of neutrinos found very difficult?
Graphical representation of (BE/A) for nucleons with mass number A.
The variation of binding energy per nucleon VS. mass number is shown in the figure:
Characteristics of Nuclear force:
(i) Nuclear forces non-central and short-ranged force.
(ii) Nuclear forces between proton-neutron and neutron-neutron are strong and attractive in nature.
b) When a heavy nucleus (A > 235 say) breaks into two lighter nuclei (nuclear fission), the binding energy per nucleon increases i.e, nucleons get more tightly bound. This implies that energy would be released in nuclear fission.
When two very light nuclei (A £10) join to form a heavy nucleus, the binding is energy per nucleon of fused heavier nucleus more than the binding energy per nucleon of lighter nuclei, so again energy would be released in nuclear fusion.
c) During the decay process of neutron, we have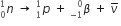
Neutrinos show weak interaction with other particles. Hence, its detection is very different.
Assume that a neutron breaks into a proton and an electron. The energy released during this process is(Mass of neutron = 1.6725 x 10–27kg; mass of proton = 1.6725 x 10–27kg; mass of electron = 9 x 10–31kg)
0.73 MeV
7.10 MeV
6.30 MeV
6.30 MeV
A.
0.73 MeV
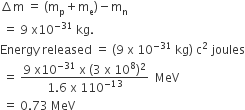
The half life of a radioactive substance is 20 minutes. The approximate time interval (t2 - t1) between the time t2 when 2/3 of it has decayed and time t1 when 1/3 of it had decayed is
14 min
20 min
28 min
28 min
B.
20 min