Answer:
(i) The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions. The ideal solutions have two other important properties. The enthalpy of mixing of the pure components to form the solution is zero and the volume of mixing is also zero, i.e.,
ΔmixH = 0
ΔmixV = 0
It means that no heat is absorbed or evolved when the components are mixed. Also, the volume of solution would be equal to the sum of
volumes of the two components.
(ii)
At molecular level, ideal behaviour of
the solutions can be explained by considering two components A and B. In pure components, the intermolecular attractive interactions will
be of types A-A and B-B, whereas in the binary solutions in addition to these two interactions, A-B type of interactions will also be present.
If the intermolecular attractive forces between the A-A and B-B are nearly equal to those between A-B, this leads to the formation of ideal
solution.
example: Solution of n-hexane and n-heptane, bromoethane and chloroethane, benzene and toluene, etc.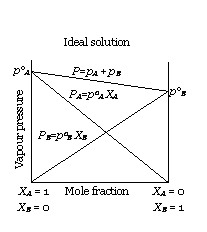
Escaping tendency of 'A' and 'B' should be same in pure liquids and in the solution.
Positive deviation from a Raoult's law:
Mixture of ethanol and cyclohexane show positive deviation when pure ethanol is added to cyclohexane the molecule of cyclohexane come in between the molecule of ethanol which result in the breaking of hydrogen bond and thus positive deviation.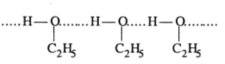
Negative deviation from Raoult's law:
Mixture of chloroform and acetone shows negtive deviation when these are mixed hydrogen bond is formed and negtive deviation is shown:
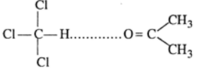
Answer:
In the same volume of water,0.1 molar of NaCl will have a greater boiling point elevation, as boiling point elevation is a colligative property which depends on the relative amount of the constituent and not on their identity.
Since more ions will be produced by NaCl (ionic compound) than glucose (covalent compound)
as there are more componets part in the NaCl molecule so the NaCl will have more boiling point.
Answer: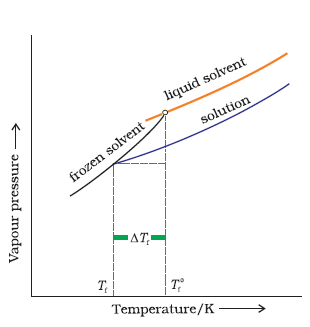
When a non-volatile solid is added to the solvent its vapour pressure decreases and now it would become equal to that of solid solvent at lower temperature. Thus, the freezing point of the solvent decreases
Answer:
It is because ethyl alchol and water do not form an ideal solution the intermolecular forces of attraction are weak so the molecules will become far apart from each other hence volume wll increase.
