Answer:
for any solution the partial vapour pressure of each volatile component in the solution is directly proportional to its mole fraction.
pA ∝ xA
Where only solvent is volatile
pA a xA where p A is vapour pressure of solvent having mole fractionxA,
But xA + xB = 1
xA = 1 – xB where xB is mole fraction of non-volatile solute B
pA = p0A (1 – xB)
= p0A – p0A x B
Total vapour pressure
Solution containing non-volatile solute : For a solution of non-volatile solid in a liquid the vapour pressure contribution by the non-volatile solute is negligible. Therefore the partial vapour pressure of a solution containing a non-volatile solute is equal to the product of the vapour pressure of the pure liquid (solvent p0A) and its mole fraction in solution.
PA = P0A x xB ....(i)
xB is the mole fraction of the non-volatile solute
B, then xA + xB = 1
xA = 1 – xB ....(ii)
Substituting the value of xA fromeq. (ii) into eq. (i), we get, pA = p0A (1 – xB) = p0A – p0A x B
Every pure liquid exerts a vapour pressure in the space above it. This is the vapour pressure of the solvent over it at that particular temperature. It depends upon the nature of the solvent and the temperature.
(a) If a volatile solute is dissolved, vapour pressure of the solvent is increased.
(b) However, if a non-volatile solute is dissolved in it, the vapour pressure of the solution is lowered. This is because, in a solution, the percentage of the volatile solvent molecules, which only contributes towards vapour pressure is diminished.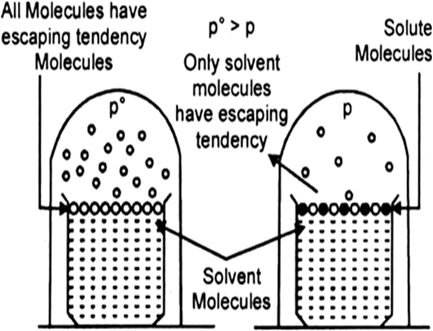
Fig. Decrease of vapour pressure when a non-volatile solute is added to the solvent.
Since, the solute molecules are non-volatile and show no measurable tendency to escape from the solution as vapour, consequently, the vapour pressure of a solution is always lower than that of its solvent.
Raoult’s gave a relation between the relative lowering of vapour pressure and the mole fraction of the solute. Mathematically:![]()
(mole fraction of the solute)
Using the above equation, we can determine the molecular weight of the solute, when the lowering in v.p. is known, when a known weight of the solute w, dissolved in a known wt. of the solvent W.p0 is the vapour pressure of the pure solvent and m and M are the molecular weights of solute and solvent respectively.
Answer:
Liquids at a given temperature vapourise and under
equilibrium conditions the pressure exerted by the vapours of the liquid over the liquid phase is called vapour pressure.
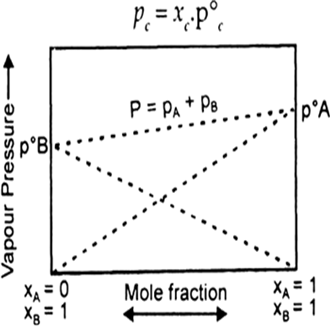
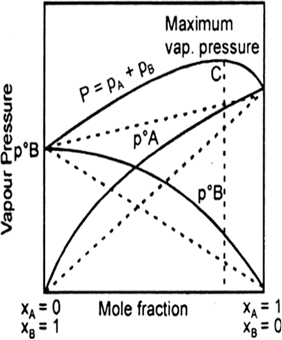
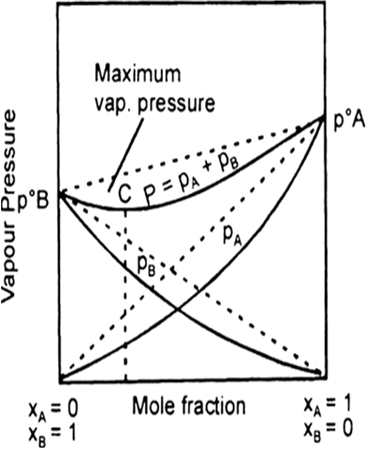
When a volatile solute is dissolved into, solvent then the vapour state solute and the solvent.
total vapour pressure above such a solution will be equal to the sum of the pressure exerted by the vapours of both solute and solvent.
Where
Ptotal = total pressure of solution
(b)
When a non- volatile solute is dissovled then there is lowering in vapour pressure .
The lowering in vapour pressureisgiven by
