A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles area required to cover a floor of area 1080 m2?
(If required you can split the tiles in whatever way want to fill up the corners.)
Area of a parallelograms = Base x Corresponding height
Area of a tile =
∴ Area of the floor = 1080 m2
Now, number of tiles = 
= 
= 45000 tiles
The shape of a garden is rectangular in the middle and semi-circular at the ends as shown in the diagram. Find the area and the perimeter of this garden. [Length of rectangle is 20 - (3.5 + 3.5) meters.]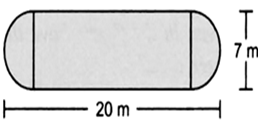
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN8036213-3.png)
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN8036213-6.png)
A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?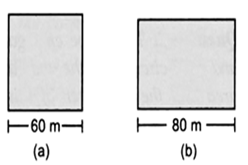
(a) Side of the square = 60 m
∴ Its perimeter = 4 x side
= 4 x 60 m
= 240 m
Area of the square = Side x Side
= 60 m x 60 m
= 3600 m2
(b) ∵ Perimeter of the rectangle = Perimeter of the given square
∴ Perimeter of the rectangle = 240 m
or 2 x [Length + Breadth] = 240 m
or 2 x [80 m + Breadth] = 240 m
or 80 m + Breadth = 
∴ Breadth = (120 - 80) m = 40 m
Now, Area of the rectangle = Length x Breadth
= 80 m x 40 m
= 3200 m2
Since, 3600 m2 > 3200 m2
∴ Area of the square field (a) is greater.
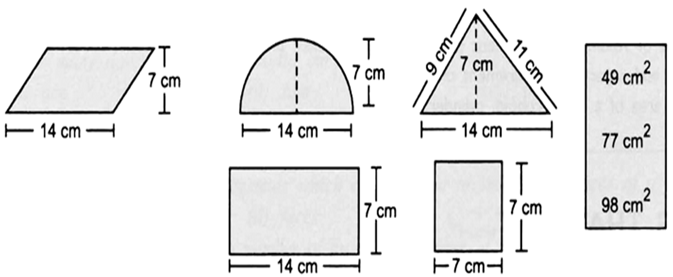
(a)
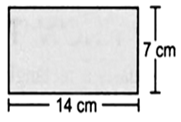
(b) (i) The given figure is a rectangle in which
Length = 14 cm
Breadth = 7 cm
∵ Perimeter of a rectangle = 2 x [Length + Breadth]
∴ Perimeter of the given figure = 2 x [14 cm + 7 cm]
= 2 x 21 cm
= 42 cm
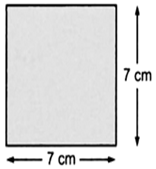
(ii) The figure is a square housing its side as 7 cm.
∵ Perimeter of a square = 4 x side
∴ Perimeter of the given figure = 4 x 7 cm
= 28 cm.
Mrs. Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of Rs 55 per m2.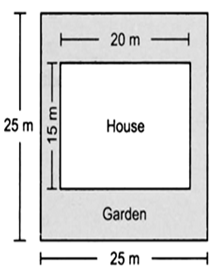
∵ The given plot is a square with side as 25 m.
∴ Area of the plot = Side x Side
= 25 m x 25 m = 625 m2
∵ The constructed portion is a rectangle having length = 20 m and breadth = 15 m.
∴ Area of the constructed portion = 20 m x 15 m
= 300 m2
Now area of the garden = [Total plot area] - [Total constructed area]
= (625 - 300)m2
= 325 m2
∴ Cost of developing the garden = Rs 55 x 325
= Rs 17, 875
Switch
