Is 216 a perfect cube? What is the number whose cube is 216?
We have 216
i.e. Resolving 216 into prime factors we have: 216 = 2 x 2 x 2 x 3x 3 x 3
i.e. 216 can be resolved in to such prime factor which can be grouped into triple of equal of factor and no factor is left over.
∴ 216 is a perfect cube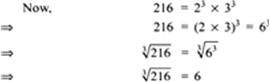
Thus, the required number is 6, whose cube is 216.
Is 1372 a perfect cube? If not, find the smallest natural number by which 1372 must be multipled so that the product is a perfect cube.
We have 1372 = 2 x 2 x 7 x 7 x 7
Since, the prime factor 2 does not appear in a group of triples. 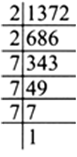
∴ 1372 is not a perfect cube.
Obviously, to make it a perfect cube we need one more 2 as its factor.
i.e. [1372] x 2 = [2 x 2 x 7 x 7 x 7] x 2
or 2744 = 2 x 2 x 2 x 7 x 7 x 7
which is a perfect cube.
Thus, the required smallest number = 2.
500 = 5 x 5 x 5 x 2 x 2
∵ In the above prime factorisation 2 x2 remain after grouping the prime factors in
triples.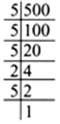
∴ 500 is not a perfect cube.
We hve 31944 = 2 x 2 x 2 x 3 x 11 x 11 x 11
Since, the prime factors of 31944 do not appear in triples as 3 is left over.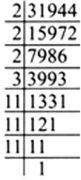
∴ 31944 is not a perfect cube, Obviously, 31944 ![]() will be a perfect cube
will be a perfect cube
i.e. [31944] ![]() 3 = [2 x 2 x 2 x 3 x 11 x 11 x 11]
3 = [2 x 2 x 2 x 3 x 11 x 11 x 11]![]() 3
3
or 10648 = 2 x 2 x 2 x 11 x 11 x 11
∴ 10648 is a perfect cube.
Thus, the required least number = 3.
