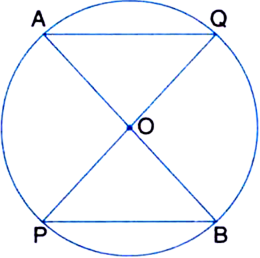
Given: In figure, a diameter AB of a circle bisects a chord PQ. AQ || PB.
To Prove: The chord PQ is also a diameter of the circle.
Proof: ∠AQP = ∠ABP ...(1)
| Angles in the same segment
∵ AQ || PB and QP intersects them
∴ ∠AQP = ∠QPB ...(2)
| Alt. Int. ∠s
From (1) and (2),
∠ABP = ∠QPB
⇒ ∠OBP = ∠OPB
∴ OP = OB ...(3)
| Sides opp. to equal angles
Again,
⇒ ∠BPQ = ∠BAQ ...(4)
| Angles in the same segment
∵ AQ || PB
and AB intersects them
∴ ∠BPQ = ∠PQA ...(5)
| Alt. Int. ∠s
From (4) and (5),
∠BAQ = ∠PQA
⇒ ∠OAQ = ∠OQA
∴ OQ = OA ...(6)
| Sides opp. to equal angles
Adding (3) and (6), we get
OP + OQ = OB + OA
⇒ PQ = AB
∵ AB is a diameter of the circle
∴ PQ is also a diameter of the circle.
AC and BD are chords of a circle which bisect each other. Prove that:
(i) AC and BD are diameters.
(ii) ABCD is a rectangle.
Given: AC and BD are chords of a circle which bisect each other at O. (say).
To Prove: (i) AC and BD are diameters
(ii) ABCD is a rectangle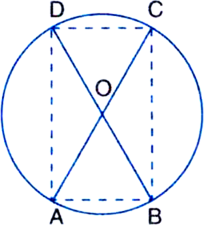
Construction: Join AB, BC, CD, and DA.
Proof: (i) In ∆OAB and ∆OCD,
OA = OC
| ∵ O is the mid-point of AC
∠AOB = ∠COD
| Vertically opposite angles
OB = OD
| ∵ O is the mid-point of BD
∴ ∆OAB ≅ ∆OCD
| SAS congruence rule
∴ AB = CD | C.P.C.T![]()
| If two chords of a circle are equal, then their corresponding arcs are congruent
In ∆OAD and ∆OCB,
OA = OC
| ∵ O is the mid-point of AC
∠AOD = ∠COB
| Vertically opposite angles
OD = OB
| ∵ O is the mid-point of BD
∴ ∆OAD = ∆OCB
| SAS congruence rule
∴ AD = CB | C.P.C.T.![]()
| If two chords of a circle are equal, then their corresponding arcs are congruent
From (1) and (2),![]()
⇒ BD divides the circle into two equal parts.
⇒ BD is a diameter.
Similarly, we can show that AC is a diameter.
(ii) ABCD is a parallelogram
| ∵ AB = DC and AD = BC (A quadrilateral is a parallelogram if both the pairs of opposite sides are equal)
∠ADB = 90°
| Angle in a semi-circle is 90°
∴ ABCD is a rectangle
| A parallelogram with one of its angles 90° is a rectangle
Given: ABCD is a cyclic trapezium with AD || BC. ∠B = 70°.
To determine: Other three angles of the trapezium.
Determination:
∠B + ∠D = 180°
| ∵ Opposite angles of a cyclic quadrilateral are supplementary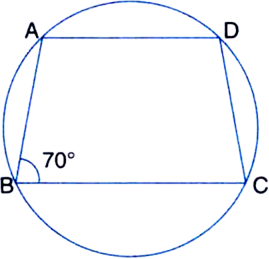
⇒ 70° + ∠D =180°
⇒ ∠D = 180° - 70°
⇒ ∠D = 110°
Again, ∵ AD || BC and transversal AB intersects them
∵ ∠A + ∠B = 180°
| ∵ The sum of the consecutive interior angles on the same side of a transversal is 180°
⇒ ∠A + 70° = 180°
⇒ ∠A = 180° - 70°
⇒ ∠A = 110°
Also, ∠A + ∠C = 180°
| ∵ Opposite angles of a cyclic quadrilateral are supplementary
⇒ 110° + ∠C = 180°
⇒ ∠C = 180° - 110°
⇒ ∠C = 70°.
Given: ABCD is trapezium in which AD = BC
To prove: Opposite angles of ABCD are supplementary.
Construction: Draw BE || AD
Proof: ∵ Quadrilateral ABED is a parallelogram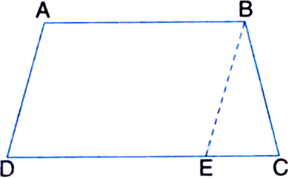
AB || DC (Given) AD || BE (By construction).
| A quadrilateral is a parallelogram if its any pair of opposite sides are parallel and equal.
∴ ∠BAD = ∠BED
| Opposite angles of a parallelogram are equal
and AD = BE
| Opposite sides of a parallelogram are equal
But AD = BC | Given
∴ BE = BC
∴ ∠BEC = ∠BCE
| Angles opposite to equal sides of a triangle are equal
∴ ∠BEC + ∠BED = 180° | Linear pair
⇒ ∠BCE + ∠BED = 180°
⇒ ∠BAD + ∠BED = 180°
⇒ ∠ADE + ∠ABE = 180°
⇒ Opposite angles of ABCD are supplementary.
Given: ABCD is a cyclic quadrilateral with AD || BC.
To Prove: AB = DC.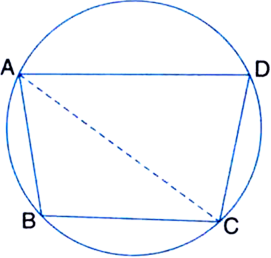
Construction: Join AC.
Proof: ∵ AD || BC
and AC intersects them
∴ ∠ACB = ∠CAD | Alt. Int. ∠s
∴ arc AB ≅ arc CD
| Arcs opposite to equal angles are congruent
∴ chord AB = chord CD
| If two arcs of a circle are congruent, then their corresponding chords are equal
⇒ AB = CD
⇒ AB = DC.
Aliter:
Given: ABCD is a cyclic quadrilateral with AD || BC.
To Prove: AB = DC.
Construction: Draw DE || AB.
Proof: AD || BC | Given
⇒ AD || BE
AB || DE | By const.
∴ Quadrilateral ADEB is a parallelogram
∴ AB = DE ...(1)
| Opp. sides of a || gm are equal
and ∠BAD = ∠BED ...(2)
| Opp. ∠s of a || gm are equal
∵ ABCD is a cyclic quadrilateral
∴ ∠BAD + ∠BCD = 180° ...(3)
| ∵ Opposite angles of a cyclic quadrilateral are supplementary
∠BED + ∠CED = 180° | Linear pair
⇒ ∠BAD + ∠CED = 180° ...(4)
| From (2)
From (3) and (4),
∠BCD = ∠CED
⇒ ∠ECD = ∠CED
∴ DE = DC
| Sides opp. to equal angles
⇒ AB = DC. | From(1)
