 Multiple Choice Questions
Multiple Choice QuestionsTwo sides of a rhombus are along the lines, x−y+1=0 and 7x−y−5=0. If its diagonals intersect at (−1, −2), then which one of the following is a vertex of this rhombus?
(−3, −9)
(−3, −8)
(1/3, -8/3)
(1/3, -8/3)
The centres of those circles which touch the circle, x2+y2−8x−8y−4=0, externally and also touch the x-axis, lie on:
a circle
an ellipse which is not a circle
a hyperbola.
a hyperbola.
The number of points having both coordinates as integers that lie in the interior of the triangle with vertices (0,0), (0,41) and (41,0) is
901
861
820
820
At present, a firm is manufacturing 2000 items. It is estimated that the rate of change of production P with respect to the additional number of workers x is given by 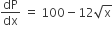 . If the firm employs 25 more workers, then
. If the firm employs 25 more workers, then
the new level of production of items is
2500
3000
3500
3500
