 Multiple Choice Questions
Multiple Choice QuestionsIf all the words (with or without meaning) having five letters, formed using the letters of the word SMALL and arranged as in a dictionary; then the position of the word SMALL is:
46th
59th
52nd
52nd
If the 2nd, 5th and 9th terms of a non-constant A.P. are in G.P., then the common ratio of this G.P. is:
8/5
4/3
1
1
If the sum of the first ten terms of the series,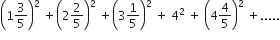 is 16/5 m, the m is equal to
is 16/5 m, the m is equal to
102
101
100
100
Three positive numbers form an increasing GP. If the middle term in this GP is doubled, then new numbers are in AP. Then, the common ratio of the GP is
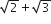
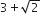
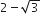
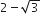
If x, y, z are in A.P. and tan−1 x, tan−1 y and tan−1 z are also in A.P., then
x= y= z
2x =3y = 6z
6x = 3y= 2z
6x = 3y= 2z
Statement 1: The sum of the series 1 + (1 + 2 + 4) + (4 + 6 + 9) + (9 + 12 + 16) + ...... + (361 + 380 +400) is 8000.
Statement 2: 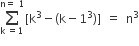 , for any natural number n.
, for any natural number n.
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
If 100 times the 100th term of an AP with non zero common difference equals the 50 times its 50th term, then the 150th term of this AP is
–150
150
times its 50th term
times its 50th term
Let x1, x2, ......, xn be n observations, and let  be their arithmetic mean and σ2 be their variance.
be their arithmetic mean and σ2 be their variance.
Statement 1: Variance of 2x1, 2x2, ......, 2xn is 4 σ2.
Statement 2: Arithmetic mean of 2x1, 2x2, ......, 2xn is 4 .
.
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
