 Multiple Choice Questions
Multiple Choice QuestionsLet C be the circle with centre at(1,1) and radius 1. If T is the circle centred at (0,y) passing through origin and touching the circle externally, then the radius of T is equal to
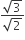
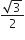
1/2
1/2
A bird is sitting on the top of a vertical pole 20m high and its elevation from a point O n the ground is 45o. It flies off horizontally straight away from the point O. After 1s, the elevation of the bird from O is reduced to 30o. Then, the speed (in m/s of the bird is
(



A ray of light along  get reflected upon reaching X -axis, the equation of the reflected ray is
get reflected upon reaching X -axis, the equation of the reflected ray is
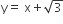
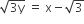


The number of values of k, for which the system of equations
(k+1) x + 8y = 4k
kx + (k+3)y = 3k -1
has no solution, is
infinite
1
2
2
In a ∆PQR, if 3 sin P + 4 cos Q = 6 and 4 sin Q + 3 cos P = 1, then the angle R is equal to
5π/6
π/6
π/4
π/4
An equation of a plane parallel to the plane x – 2y + 2z – 5 = 0 and at a unit distance from the origin is
x – 2y + 2z – 3 = 0
x – 2y + 2z + 1 = 0
x – 2y + 2z – 1 = 0
x – 2y + 2z – 1 = 0
If the line 2x + y = k passes through the point which divides the line segment joining the points (1, 1) and (2, 4) in the ratio 3 : 2, then k equals
29/5
5
6
6
Three numbers are chosen at random without replacement from {1, 2, 3, ...... 8}. The probability that their minimum is 3, given that their maximum is 6, is
3/8
1/5
1/4
1/4
