 Multiple Choice Questions
Multiple Choice QuestionsA combination of capacitors is set up as shown in the figure. The magnitude of the electric field, due to a point charge Q (having a charge equal to the sum of the charges on the 4 µF and 9 µF capacitors), at a point distant 30 m from it, would equal: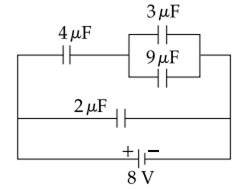
240N/C
360N/C
420N/C
420N/C
A uniformly charged solid sphere of radius R has potential V0 (measured with respect to ∞) on its surface. For this sphere, the equipotential surfaces with potentials 3Vo/2, 5Vo/4, 3V/4 and Vo/4 have radius R1, R2,R3 and R4 respectively. Then
R1 = 0 and R2>(R4-R3)
R1≠0 and (R2-R1)>(R4-R3)
R1 = 0 and R2<(R4-R3)
R1 = 0 and R2<(R4-R3)
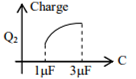
In the given circuit, charge Q2 on the 2 μF capacitor changes as C is varied from 1 μF to 3 μF. Q2 as a function of ‘C’ is given properly by : (figures are drawn schematically and are not to scale)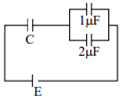
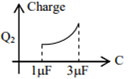
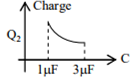
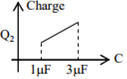
Assume that an electric field 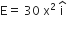 exists in space. Then the potential difference VA – VO, where VO is the potential at the origin and VA the potential at x = 2 m is:
exists in space. Then the potential difference VA – VO, where VO is the potential at the origin and VA the potential at x = 2 m is:
120 J
-120 J
-80 J
-80 J
A parallel plate capacitor is made of two circular plates separated by a distance of 5 mm and with a dielectric of dielectric constant 2.2 between them. When the electric field in the dielectric is 3 × 104 V/m, the charge density of the positive plate will be close to
6 x 10-7 C/m2
3 x 10-7 C/m2
3 x 104 C/m2
3 x 104 C/m2
Two capacitors C1 and C2 are charged to 120 V and 200 V respectively. It is found that by connecting them together the potential on each one can be made zero. Then
5C1 = 3C2
3C1 = 5C2
3C1 = 5C2 = 0
3C1 = 5C2 = 0
The figure shows an experimental plot for discharging of a capacitor in an R-C circuit. The time constant τ of this circuit lies between
150 sec and 200 sec
0 and 50 sec
50 sec and 100 sec
50 sec and 100 sec
A fully charged capacitor C with initial charge q0 is connected to a coil of self inductance L at t = 0. The time at which the energy is stored equally between the electric and the magnetic fields is
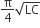



The electrostatic potential inside a charged spherical ball is given by Φ = ar2 + b where r is the distance from the centre; a,b are constants. Then the charge density inside the ball is
-6aε0r
-24πaε0
-6aε0
-6aε0
Let C be the capacitance of a capacitor discharging through a resistor R. Suppose t1 is the time taken for the energy stored in the capacitor to reduce to half its initial value and t2 is the time taken for the charge to reduce to one–fourth its initial value. Then the ratio t1/t2 will be
1
1/2
1/4
1/4
