 Multiple Choice Questions
Multiple Choice QuestionsAn ideal gas undergoes a quasi static, reversible process in which its molar heat capacity C remains constant. If during this process the relation of pressure P and volume V is given by PVn=constant, then n is given by (Here CP and CV are molar specific heat at constant pressure and constant volume, respectively):
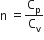
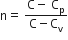
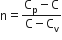
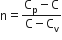
‘n’ moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be: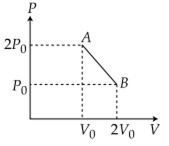
![]()
![]()
![]()
![]()
Three rods of Copper, Brass and Steel are welded together to from a Y –shaped structure. Area of cross – section of each rod = 4 cm2. End of the copper rod is maintained at 100oC where as ends of brass and steel are kept at 0oC. Lengths of the copper, brass and steel rods are 46, 13 and 12 cms respectively. The rods are thermally insulated from surroundings except at ends. Thermal conductivities of copper, brass and steel are 0.92, 0.26 and 0.12 CGS units respectively. Rate of heat flow through copper rod is:
1.2 cal/s
2.4 cal/s
4.8 cal/s
4.8 cal/s
Assume that a drop of liquid evaporates by decrease in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible? The surface tension is T, the density of liquid is ρ and L is its latent heat of vaporisation.
ρL/T

T/ρL
T/ρL
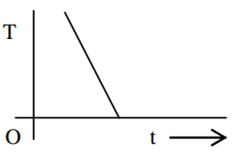
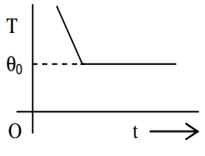
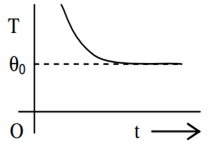
If a piece of metal is heated to temperature θ and then allowed to cool in a room which is at temperature θ0 the graph between the temperature T of the metal and time t will be closest to

100g of water is heated from 30°C to 50°C ignoring the slight expansion of the water, the change in its internal energy is (specific heat of water is 4184 J/Kg/K)
8.4 kJ
84 kJ
2.1 kJ
2.1 kJ
A thermally insulated vessel contains an ideal gas of molecular mass M and ratio of specific heat γ.It is moving with speed v and it suddenly brought to rest. Assuming no heat is lost to the surroundings, its temperature increases by
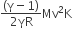
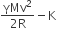
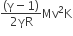
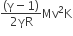
Two conductors have the same resistance a 0°C but their temperature coefficients o resistance are α1 and α2. The respective temperature coefficients of their series parallel combinations are nearly
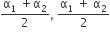
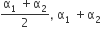
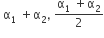
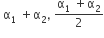
The temperature of an open room of volume 30 m3 increases from 17°C to 27°C due to sunshine. The atmospheric pressure in the room remains 1 × 105 Pa. If ni and nf are the numbers of molecules in the room before and after heating, then nf – ni will be
2.5 x 1025
-2.5 x 1025
-1.61 x 1023
-1.61 x 1023
A copper ball of mass 100 gm is at a temperature T. It is dropped in a copper calorimeter of mass 100 gm, filled with 170 gm of water at room temperature. Subsequently, the temperature of the system is found to be 75°C. T is given by:(Given : room temperature = 30° C, specific heat of copper = 0.1 cal/gm°C
1250°C
825°C
800°C
800°C
