 Multiple Choice Questions
Multiple Choice QuestionsRate law for the reaction, A+ B → product is rate = k[A]2[B] What is the rate constant; if rate of reaction at a given temperature is 0.22 Ms-1, when [A]= 1 M band [BJ= 0.25 M?
3.52 M-2s-1
0.88 M-2s-1
1.136 M-2s-1
0.05 M-2s-1
Decomposition of H2O2 follows a first order reaction. In fifty minutes the concentration of H2O2 decreases from 0.5 to 0.125 M in one such decomposition. When the concentration of H2O2 reaches 0.05 M, the rate of formation of O2 will be:
6.93×10−4 mol min−1
2.66 L min−1 at STP
1.34×10−2 mol min−1
1.34×10−2 mol min−1
Higher order (>3) reactions are rare due to:
the increase in entropy and activation energy as more molecules are involved.
shifting of equilibrium towards reactants due to elastic collisions
loss of active species on a collision
loss of active species on a collision
The resistance of 0.2 M solution of an electrolyte is 50 Ω. The specific conductance of the solution of 0.5 M solution of the same electrolyte is 1.4 S m-1 and resistance of the same solution of the same electrolyte is 280 Ω. The molar conductivity of 0.5 M solution of the electrolyte in Sm-2 mol-1 is
5 x 10-4
5 x 10-3
5 x 103
5 x 103
For the non- stoichiometric reaction 2A + B → C + D, the following kinetic data were obtained in three separate experiment, all at 298 K.
| Initial concentration (A) | Initial concnetration (B) | Initial rate of formation of C (mol L-1 S-1) | |
| 1 | 0.1 M | 0.1 M | 1.2 x 10-3 |
| 2 | 0.1 M | 0.2 M | 1.2 x 10-3 |
| 3 | 0.2 M | 0.1 M | 2.4 x 10-3 |
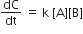
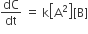
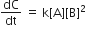
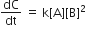
The rate of a reaction doubles when its temperature changes from 300K to 310K. Activation energy of such a reaction will be (R = 8.314 JK–1 mol–1 and log 2 = 0.301)
53.6 kJ mol-1
48.6 kJ mol-1
58.5 kJ mol-1
58.5 kJ mol-1
For a first order reaction, (A) → products, the concentration of A changes from 0.1 M to 0.025 M in 40 minutes. The rate of reaction when the concentration of A is 0.01 M is
1.73 x 10–5 M/ min
3.47 x 10–4 M/min
3.47 x 10–5 M/min
3.47 x 10–5 M/min
The rate of a chemical reaction doubles for every 10ºC rise of temperature. If the temperature is raised by 50ºC, the rate of the reaction increases by about
10 times
24 times
32 times
32 times
The time for half life period of a certain reaction A → Products is 1 hour. When the initial concentration of the reactant ‘A’ is 2.0 mol L–1, how much time does it take for its concentration to come from 0.50 to 0.25 mol L–1 if it is a zero order reaction?
1 h
4 h
0.25 h
0.25 h
Two reactions R1 and R2 have identical pre-exponential factors. Activation energy of R1 exceeds that of R2 by 10 kJ mol–1. If k1 and k2 are rate constants for reactions R1 and R2 respectively at 300 K, then ln(k2/k1) is equal to-
(R = 8.314 J mol–1K–1)
8
12
6
6
