 Multiple Choice Questions
Multiple Choice QuestionsGiven in the figure are two blocks A and B of weight 20 N and 100 N respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is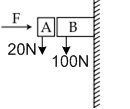
100N
80 N
120 N
150 N
A particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to
44%
50%
56%
62%
A mass ‘m’ is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall on release?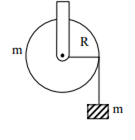
2g/3
g/2
5g/6
5g/6
A block of mass m is placed on a surface with a vertical cross-section given by y = x3/6. If the coefficient of friction is 0.5, the maximum height above ground at which the block can be placed without slipping is
A thin liquid film formed between a U-shaped wire and a light slider supports a weight of 1.5 x10–2N (see figure). The length of the slider is 30 cm and its weight negligible. The surface tension of the liquid film is
0.0125 Nm-1
0.1 Nm-1
0.05 Nm-1
0.05 Nm-1
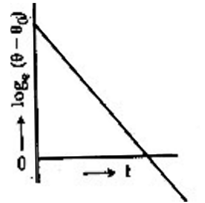
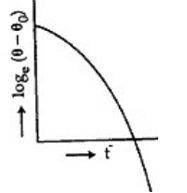
A liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge (θ – θ0) and t is


A mass m hangs with the help of a string wrapped around a pulley on a frictionless bearing. The pulley has mass m and radius R.Assuming pulley to be a perfect uniform circular disc, the acceleration of the mass m, if the string does not slip on the pulley, is
g
2/3g
g/3
g/3
A pulley of radius 2m is rotated about its axis by a force F = (20t - 5t2) Newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg-m2, the number of rotations made by the pulley before its direction of motion if reversed is
more than 3 but less than 6
more than 6 but less than 9
more than 9
more than 9
STATEMENT – 1
Two particles moving in the same direction do not lose all their energy in a completely inelastic collision.
STATEMENT – 2
Principle of conservation of momentum holds true for all kinds of collisions.
The statement I is True, Statement II is False.
The statement I is True, Statement II is True; Statement II is a correct explanation for Statement I.
The statement I is True, Statement II is True; Statement II is not the correct explanation for Statement I.
The statement I is True, Statement II is True; Statement II is not the correct explanation for Statement I.
Two fixed frictionless inclined planes making an angle 30° and 60° with the vertical are shown in the figure. Two blocks A and B are placed on the two planes. What is the relative vertical acceleration of A with respect to B?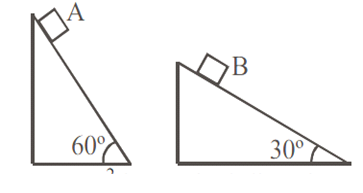
4.9 ms-2 in horizontal direction
9.8 ms-2 in vertical direction
zero
zero
