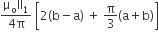Multiple Choice Questions
Multiple Choice QuestionsTwo identical wires A and B, each of length ‘l’, carry the same current I. Wire A is bent into a circle of radius R and wire B is bent to form a square of side ‘a’. If BA and BB are the values of the magnetic field at the centres of the circle and square respectively, then the ratio BA /BB is:
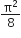
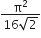
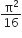
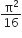
Hysteresis loops for two magnetic materials A and B are given below: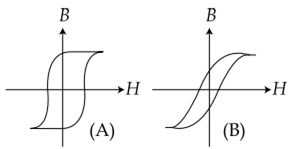
These materials are used to make magnets for electric generators, transformer core and electromagnet core. Then it is proper to use:
A for electric generators and transformers.
A for electromagnets and B for electric generators
A for transformers and B for electric generators.
A for transformers and B for electric generators.
An arc lamp requires a direct current of 10 A at 80 V to function. If it is connected to a 220 V (rms), 50 Hz AC supply, the series inductor needed for it to work is close to:
80 H
0.08 H
0.044 H
0.044 H
A galvanometer having a coil resistance of 100 Ω gives a full-scale deflection, when a current of 1 mA is passed through it. The value of the resistance, which can convert this galvanometer into ammeter giving a full-scale deflection for a current of 10 A, is:
0.01 Ω
2 Ω
0.1 Ω
0.1 Ω
Two coaxial solenoids of different radii carry current I in the same direction. Let 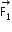 be the magnetic force on the inner solenoid due to the outer one and
be the magnetic force on the inner solenoid due to the outer one and 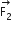 be the magnetic force on the outer solenoid due to the inner one. Then:
be the magnetic force on the outer solenoid due to the inner one. Then:
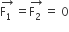
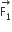 is radially inwards and
is radially inwards and 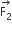 is radially outwards
is radially outwards
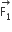 is radially inwards and
is radially inwards and 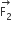 =0
=0
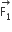 is radially inwards and
is radially inwards and  =0
=0
A rectangular loop of sides 10 cm and 5 cm carrying a current I of 12 A is placed in different orientations as shown in the figures below: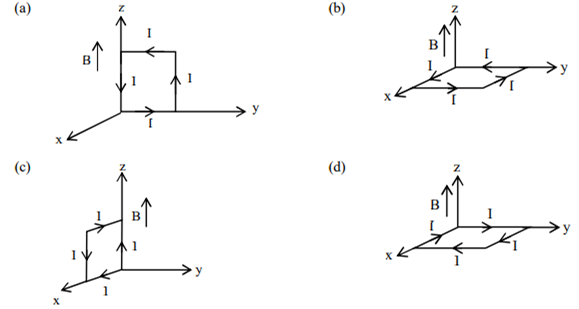
If there is a uniform magnetic field of 0.3 T in the positive z direction , in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium?
(a) and (b) respectively
(a) and (c) respectively
(b) and (d) respectively
(b) and (d) respectively
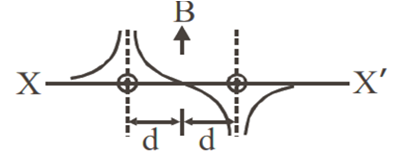
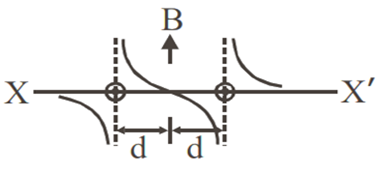
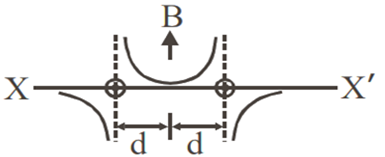
Two long parallel wires are at a distance 2d apart. They carry steady equal currents flowing out of the plane of the paper as shown. The variation of the magnetic field B along the line XX' is given by




In a coil of resistance 100 Ω, a current is induced by changing the magnetic flux through it as shown in the figure. The magnitude of change in flux through the coil is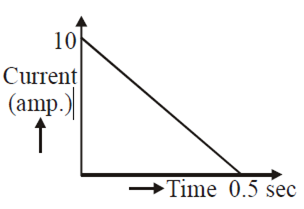
250 Wb
275 Wb
200 Wb
200 Wb
A current loop ABCD is held fixed on the plane of the paper as shown in the figure. The arcs BC (radius = b) and DA (radius = a) of the loop are joined by two straight wires AB andCD. A steady current I is flowing in the loop. Angle made by AB and CD at the origin O is 30º. Another straight thin wire with steady current I1 flowing out of the plane of the paper is kept at the origin.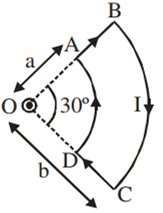
The magnitude of the magnetic field (2) due to the loop ABCD at the origin (O) is
zero
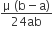
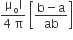
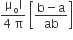
A current loop ABCD is held fixed on the plane of the paper as shown in the figure. The arcs BC (radius = b) and DA (radius = a) of the loop are joined by two straight wires AB andCD. A steady current I is flowing in the loop. Angle made by AB and CD at the origin O is 30º. Another straight thin wire with steady current I1 flowing out of the plane of the paper is kept at the origin.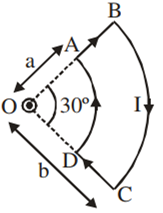
Due to the presence of the current I1 at the origin
The magnitude of the magnetic field (2) due to the loop ABCD at the origin (O) is
The forces on AB and DC are zero
The forces on AD and BC are zero
The magnitude of the net force on the loop is given by 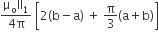
The magnitude of the net force on the loop is given by