 Multiple Choice Questions
Multiple Choice QuestionsA student measures the time period of 100 oscillations of a simple pendulum four times. The data set is 90 s, 91 s, 95 s and 92 s. If the minimum division in the measuring clock is 1 s, then the reported mean time should be:
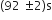
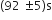
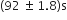
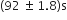
A pendulum clock loses 12 s a day if the temperature is 408C and gains 4 s a day if the temperature is 208C. The temperature at which the clock will show correct time, and the co-efficient of linear expansion (α) of the metal of the pendulum shaft are respectively:
25 C; α=1.85×10−5/ °C
60 °C; α=1.85×10−4/ °C
30°C; α=1.85×10−3/°C
30°C; α=1.85×10−3/°C
A particle performs simple harmonic motion with amplitude A. It's speed is trebled at the instant that it is at a distance 2A/3 from the equilibrium position. The new amplitude of the motion is:

3A


The period of oscillation of a simple pendulum is ![]() . The measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using wrist watch of 1 s resolution. The accuracy in the determination of g is:
. The measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using wrist watch of 1 s resolution. The accuracy in the determination of g is:
2%
3%
1%
5%
For a simple pendulum, a graph is plotted between its kinetic energy (KE) and potential energy (PE) against its displacement d. Which one of the following represents these correctly?
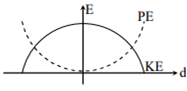
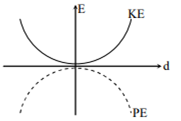
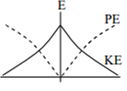
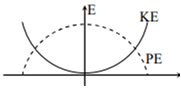
A particle moves with simple harmonic motion in a straight line. In first τ s, after starting from rest it travels a distance a, and in next τ s it travels 2a, in the same direction, then
amplitude of motion is 3a
time period of oscillations is 8τ
amplitude of motion is 4a
amplitude of motion is 4a
A pipe of length 85 cm is closed from one end. Find the number of possible natural oscillations of the air column in the pipe whose frequencies lie below 1250 Hz. The velocity of sound in air is 340 m/s.
12
8
6
6
A uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density σ at the equilibrium position. The extension x0 of the spring when it is in equilibrium is
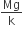
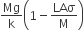
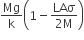
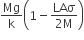
The amplitude of a damped oscillator decreases to 0.9 times its original magnitude is 5s. In another 10s it will decrease to α times its original magnitude, where α equals
0.7
0.81
0.729
0.729
If a simple pendulum has the significant amplitude (up to a factor of 1/e of original) only in the period between t = Os to t = τs, then τ may be called the average life of the pendulum. When the spherical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity, with 'b' as the constant of proportionality, the average life time of the pendulum is (assuming damping is small) in seconds:
0.693/b
b
1/b
1/b
