The combined resistance R of two resistors R₁ and R₂ (R₁ , R₂ > 0) is given by .
If R₁ + R₂ = C (a constant), show that the maximum resistance R is obtained by choosing R₁ = R₂.

322.

Show that the rectangle of maximum perimeter which can be inscribed in a circle of radius is a square of side 

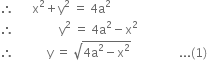
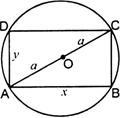
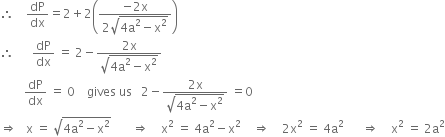
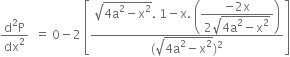
Show that the surface area of a closed cuboid with square base and given volume is minimum when it is a cube.

Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic
centimetres, find the dimensions of the can which has the minimum surface
area?
Or
Of all the closed cylindrical tin cans (right circular) which enclose a given volume of 100 cubic cm., which has the minimum surface area?

Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.

Show that a cylinder of given volume open at the top has minimum total surface area provided its height is equal to the radius of its base.

Show that the height of the cylinder, open at the top, of given surface area and greatest volume is equal to the radius of its base.

A rectangle is inscribed in a semi-circle of radius r with one of its sides on the diameter of the semi-circle. Find the dimensions of the rectangle so that its area is maximum Find also this area.

Show that the height of the cone of maximum volume that can be inscribed in a sphere of radius 12 cm is 16 cm.