Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Application of Derivatives

Name: Zigya - For The Curious Learner
Rating: 4.4 (740 reviews)

Long Answer Type

331. A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m^3. If building of tank costs Rs. 70 per sq. metres for the base and Rs. 45 per square metre for sides. What is the cost of least expensive tank ?

92 Views

Short Answer Type

332.
Show that the height of a closed right circular cylinder of given volume and least surface area is equal to its diameter.

Let r be the radius of base of circular cylinder and h be its height. Let V be the volume and S be the total surface area.

therefore space space space space space straight V space equals space πr squared straight h space space space space space space space space space space space space space space rightwards double arrow space space space straight h space equals straight V over πr squared

...(1)
Also,

straight S space equals space 2 πrh plus 2 πr squared space equals space 2 πr. space straight V over πr squared plus 2 πr squared

open square brackets because space space of space left parenthesis 1 right parenthesis close square brackets

therefore space space straight S space equals fraction numerator 2 space straight V over denominator straight r end fraction plus 2 πr squared therefore space space space dS over dr space equals negative fraction numerator 2 straight V over denominator straight r squared end fraction plus 4 πr Now space dS over dr equals 0 space space space rightwards double arrow space space space space fraction numerator negative 2 straight V over denominator straight r squared end fraction plus 4 space straight pi space straight r space equals space 0 space space space space space space space space rightwards double arrow space space space space 2 space straight V space equals space 4 πr cubed

rightwards double arrow space space space 2 πr squared straight h space equals space 4 πr cubed

open square brackets because space space space straight V space equals space πr squared straight h close square brackets

rightwards double arrow space space space straight r space equals space straight h over 2

Now,

fraction numerator straight d squared straight S over denominator dr squared end fraction space equals space fraction numerator 4 straight V over denominator straight r squared end fraction plus 4 straight pi

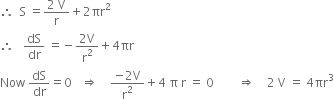
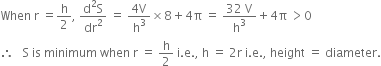
When space straight r space equals straight h over 2 comma space fraction numerator straight d squared straight S over denominator dr squared end fraction space equals space fraction numerator 4 straight V over denominator straight h cubed end fraction cross times 8 plus 4 straight pi space equals space fraction numerator 32 space straight V over denominator straight h cubed end fraction plus 4 straight pi space greater than 0 therefore space space space straight S space is space minimum space when space straight r space equals space straight h over 2 space straight i. straight e. comma space straight h space equals space 2 straight r space straight i. straight e. comma space height space equals space diameter.

76 Views

Long Answer Type

333.

Prove that the radius of the right circular cylinder of greatest curved surface which can be inscribed in a given cone is half of that of the cone.

94 Views

Short Answer Type

334. Show that the height of the right circular cylinder of maximum volume that can be inscribed in a given circular cone of height h is

1 third straight h

82 Views

Long Answer Type

335.

Show that the height of a cylinder of maximum volume that can be inscribed in a sphere of radius R is a sphere of radius R is $fraction numerator 2 straight R over denominator square root of 3 end fraction.$ Also, find the maximum volume.

84 Views

Short Answer Type

336.

Find the height of a right circular cylinder of maximum volume, which can be inscribed in a sphere of radius 9 cm.

96 Views

337.

Show that the volume of the greatest cylinder which can be inscribed in a cone of height h and semi-vertical angle 30° is $4 over 81 πh cubed$

121 Views

Long Answer Type

338.

Show that height of the cylinder of greatest volume which can be inscribed in a right ciruclar cone of height h and semi vertical angle $straight alpha$ is one-third that of the cone and the greatest volume of cylinder is $4 over 27 πh cubed space tan squared straight alpha.$

86 Views

Short Answer Type

339. Find the volume of the largest cylinder that can be inscribed in a sphere of radius r.

75 Views

340.

Show that the maximum volume of the cylinder which can be inscribed in a sphere of radius $5 square root of 3 space cm space is space 500 space straight pi space cm cubed.$