Short Answer Type
Long Answer TypeUsing integration, find the area of the triangular region whose sides have the equations y = 2 x + 1, y = 3 x + 1 and x = 4.
The equations of the sides are
2 x + y - 4 = 0 ...(1)
3 x - 2 y - 6 = 0 ...(2)
x - 3 y + 5 = 0 ...(3)
Solving (1) and (2), we get
Solving (2) and (3), we get,
Solving (1) and (3), we get,
or 
From B. draw BL ⊥ x-axis and from A. draw AM ⊥ x-axis.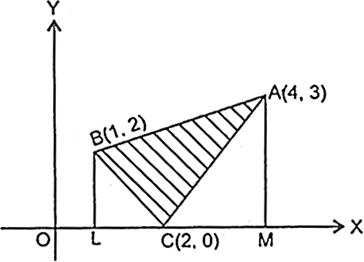
Required area = Area of 
= Area of region BLMA - area of 
- area of 
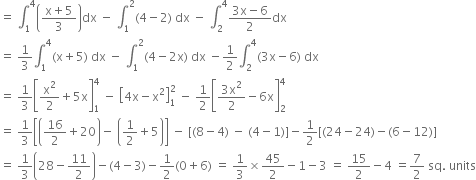
Using integration, find the area of the region bounded by the triangle whose vertices are (-1, 1), (0, 5) and (3, 2).
Short Answer TypeUsing integration, find the area of the region bounded by the triangle whose vertices are (1, 0), (2, 2) and (3, 1).
Long Answer TypeUsing integration find the area of region bounded by the triangle whose vertices are (-1, 0), (1, 3) and (3, 2).
.
Switch
