Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Conic Section

Short Answer Type

91. Find equation of parabola for vertex at origin, focus (0, –2), directrix y = 2.

84 Views

92. Find equation of parabola for vertex at origin, focus (–3, 0), directrix x = 3.

86 Views

93. Find equation of parabola for vertex at origin, axis along the y-axis and passing through the point (3, 2).

108 Views

94. Find equation of parabola for vertex at the origin, symmetric with respect to the x-axis and passing through point (2, –3).

103 Views

Long Answer Type

95.
The cable of a uniformly loaded suspension bridge hang in the form of a parabola.
The roadway which is horizontal and 100 m long, is supported by vertical wires attached to the cable, the longest wire being 30 m and the shortest being 6 m. Find the length of a supporting wire attached to a roadway 18 m from the middle.

Let AOB be the cable of a uniformly loaded suspension bridge as shown in the figure.
Let AL and BM be the longest wires of length 30 m each. Let OC be the shortest wire of length 6 m and LM be the road way as shown in the figure.

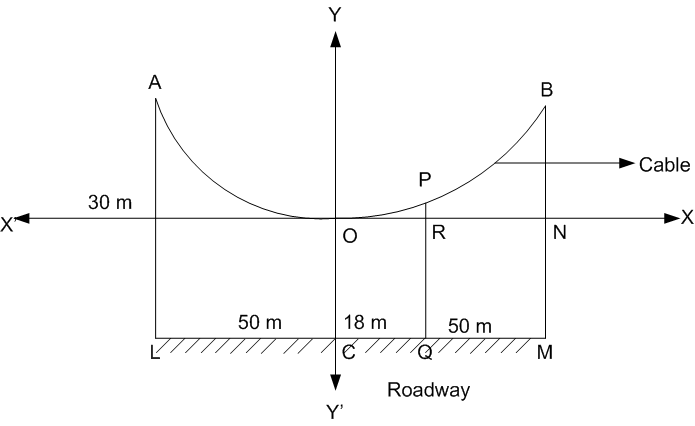
The longest supporting wire = AL = BM = 30 m
The shortest supporting cable = OC = 6 m
Length of the roadway = LM = 100 m
∴ LC = CM = 50 m
Let O be the vertex and OY be the axis of the parabola
∴ Equation of the parabola is $<pre>uncaught exception: mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56 #0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>$ ...(i)
ON = CM = 50
BN = BM - MN = BM - OC = 30 - 6 = 24
∴ Co-ordinates of point B are (50, 24)
Since it lies on the parabola (i)
∴ $left parenthesis 50 right parenthesis squared equals 4 left parenthesis straight a right parenthesis space left parenthesis 24 right parenthesis space or space straight a equals 2500 over 96 equals 625 over 24$
∴ From (i), the equation of the parabola is: $straight x squared equals 4 open parentheses 625 over 24 close parentheses straight y$
or $straight x squared equals 625 over 6 straight y$ ...(ii)
Let the length of the supporting wire PQ at a distance of 18 m be h.
∴ OR = CQ = 18 m
PR = PQ - RQ = PQ - OC = h - 6
$rightwards double arrow$ Co-ordinates of point P are (18, h - 6)
Since it lies on parabola (ii)
∴ $space space open parentheses 18 close parentheses squared space equals space 625 over 6 left parenthesis straight h minus 6 right parenthesis$
$rightwards double arrow$ $space space space space 324 cross times 6 space equals space 625 space straight h space minus space 3750$
$rightwards double arrow$ 1944 + 3750 = 625 h
$rightwards double arrow$ $straight h equals 5694 over 625 equals 9.11 space straight m$

176 Views

96. Verify that the locus of a point P which moves so that the sum of its distance from points S₁ (– 4,0) and S₂ (4,0) is 10, is an ellipse.

89 Views

97. In the following, find the co-ordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.

straight x squared over 36 plus straight y squared over 16 equals 1

91 Views

98. In the following, find the co-ordinates of the foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.

<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

99 Views

99. In the following equation, Find the co-ordinates of foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of latus rectum of the ellipse.

16 straight x squared plus straight y squared equals 16

106 Views

100. In the following equation, Find the co-ordinates of foci, the vertices, the length of major axis, the minor axis, the eccentricity and the length of latus rectum of the ellipse.

<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

100 Views