 Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeLet P be any point on the ellipseВ ![]() В with the two foci atВ
В with the two foci atВ ![]() В andВ
В andВ ![]() В Verify thatВ
В Verify thatВ ![]()
Let point P be (x, y). FocusВ ![]() В is (-c, 0), В
В is (-c, 0), В ![]() В is (c, 0)
В is (c, 0)![]() В В В В В В В В В В В В
В В В В В В В В В В В В ![]()
∴     ![]()
Now, В В В В В ![]()
But, В В В В В В В В В В В В В ![]()
∴                ![]()
∴   ![]()
![]()
В В ![]()
В В В ![]()
Hence,В ![]() , which verifies the ellipse property,В
, which verifies the ellipse property,В ![]()
For ellipseВ ![]() В verifyВ
В verifyВ ![]() В whereВ
В whereВ ![]() В andВ
В andВ ![]() В be the foci of the ellipse and P is any point on it.
В be the foci of the ellipse and P is any point on it.
 Short Answer Type
Short Answer Type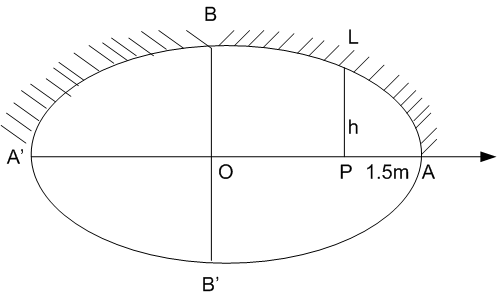
 Long Answer Type
Long Answer TypeIn the following, find the coordinates of the foci, the vertices, the lengthВ of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.![]()
In the following, find the coordinates of the foci, the vertices, the lengthВ of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.![]()
In the following, find the coordinates of the foci, the vertices, the lengthВ of major axis, the minor axis, the eccentricity and the length of the latus rectum of the ellipse.![]()
