Long Answer TypeCheck whether the points (2, 2), (4, 4) and 
lie inside, outside or on the cirlcle 
The given equation of the circle is 
The centreo of the circle is (0, 0) and radius of circle is 3
For point (2, 2).
Distance of point (2, 2) from centre (0, 0) = 
(radius of circle)
∴ Point (2, 2) lies inside the circle
For point (4, 4),
Distance of point (4, 4) from centre (0, 0) = ![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN11034907-4.png)
(radius of circle)
∴ Point (4, 4) lies outside the circle
For point 
Distance of point 
from the centre of the circle (0, 0).
(radius of the circle).
∴ Point 
lies on the circle.
Short Answer Type
Multiple Choice QuestionsThe locus of the foot of perpendicular drawn from the centre of the ellipse x2+3y2 =6 on any tangent to it is
(x2-y2)2 = 6x2+2y2
(x2-y2)2 = 6x2 -2y2
(x2+y2)2 = 6x2+2y2
(x2+y2)2 = 6x2+2y2
The slope of the line touching both the parabolas y2 = 4x and x2-32y is
1/2
3/2
1/8
1/8
The circle passing through (1,-2) and touching the axis of x at (3,0) also passes through the point
(-5,2)
(2,-5)
(5,-2)
(5,-2)
The equation of the circle passing through the foci of the ellipse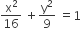 
and having centre at (0,3) is
x2+y2-6y-7 =0
x2+y2-6y+7 =0
x2+y2-6y-5 =0
x2+y2-6y-5 =0
Let Tn be the number of all possible triangles formed by joining vertices of an n-sided regular polygon. If Tn+1 − Tn = 10, then the value of n is
7
5
10
10
Given A circle, 2x2 + 2y2= 5 and parabola,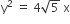 
Statement I An equation of a common tangent to these curves is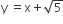 
Statement II If the line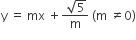 
is the common tangent, then m satisfies m4-3m2+2 =0
Statement I is true, Statement II is true; Statement II is a correct explanation for statement I
Statement I is true, Statement II is true; Statement II is not a correct explanation for statement I
Statement I is true, Statement II is false
Statement I is true, Statement II is false
Statement I An equation of a common tangent to the parabola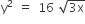 
and the ellipse 2x2 +y2 =4 is 
.
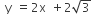Statement II If the line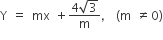 
is a common tangent to the parabola 
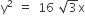and the ellipse 2x2 +y2 =4, then m satisfies m4 +2m2 =24
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Switch
