 Multiple Choice Questions
Multiple Choice QuestionsThe equation of hyperbola whose coordinates of the foci are (± 8, 0) and the length of latusrectum is 24 units, is
3x2 - y2 = 48
4x2 - y2 = 48
x2 - 3y2 = 48
x2 - 4y2 = 48
If the circle x2 + y2 + 2gx + 2fy + c = 0 cuts the three circles x2 + y2 - 5 = 0, x2 + y2 - 8x - 6y + 10 = 0 and x2 + y2 - 4x + 2y - 2 = 0 at the extremities of their diameters, then
c = - 5
fg = 147/25
g + 2f = c + 2
4f = 3g
Lines x + y = 1 and 3y = x + 3 intersect the ellipse x2 + 9y2 = 9 at the points P,Q and R. The area of the PQR is
For the variable , the locus of the point of intersection of the lines 3tx - 2y + 6t = 0 and 3x + 2ty - 6 = 0 is
The locus of the mid-points of the chords of an ellipse x2 + 4y2 = 4 that are drawn from the positive end of the minor axis, is
a circle with centre and radius 1
a parabola with focus and directrix x = - 1
an ellipse with centre , major axis and minor axis
a hyperbola with centre , transverse axis 1 and conjugate axis
A point P lies on the circle x2 + y2 = 169. If Q = (5, 12) and R = (-12, 5) then the QPR is
B.
Given equation of circle is,
x2 + y2 = 169
Its centre = ( 0, 0) and radius = 13
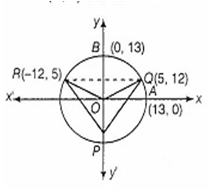
Now, slope of OR =
and slope of OQ =
We know that, angle made by the chord of circle at circumference is equal to the half of the angle made by the same chord at the centre of circle.
A point moves, so that the sum of squares of its distance from the points (1, 2) and (- 2, 1) is always 6. Then, its locus is
the straight line
a circle with centre and radius
a parabola with focus (1, 2) and directrix passing through (- 2, 1)
an ellipse with foci (1, 2) and (- 2, 1)
A circle passing through (0, 0), (2, 6), (6, 2) cut the x-axis at the point P (0, 0). Then, the lenght of OP, where O is the origin, is
5
10
For the variable t, the locus of the points of intersection of lines x - 2y = t and x + 2y = is
the straight line x = y
the circle with centre at the origin and radius 1
the ellipse with centre at the origin and one focus
the hyperbola with centre at the origin and one
If one end of a diameter of the circle 3x2 + 3y2 - 9x + 6y + y = 0 is (1, 2), then the other end is
(2, 1)
(2, 4)
(2, - 4)
(- 4, 2)
