 Long Answer Type
Long Answer TypeUsing matrices solve the following system of linear equations:
x - y + 2 z = 7
3 x + 4 y - 5 z = - 5
2 x - y + 3 z = 12
 Multiple Choice Questions
Multiple Choice QuestionsThe system of linear equations x+λy−z=0; λx−y−z=0; x+y−λz=0 has a non-trivial solution for
infinitely many values of λ.
exactly one value of λ.
exactly two values of λ.
exactly two values of λ.
D.
exactly two values of λ.
Given system of linear equations isÂ
x+λy−z=0;
λx−y−z=0;
x+y−λz=0Â
Note that, given system will have a non-trivial solution only if the determinant of the coefficient matrix is zero, ie.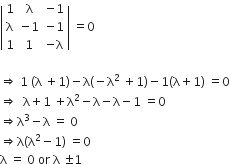
Hence, given system of linear equation has a non-trivial solution for exactly three values of λ.
A =Â 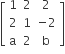 Â is a matrix satisfying the equation AAT = 9I, Where I is 3 x 3 identity matrix, then the ordered pair (a,b) is equal to
 is a matrix satisfying the equation AAT = 9I, Where I is 3 x 3 identity matrix, then the ordered pair (a,b) is equal to
(2,-1)
(-2,1)
(2,1)
(2,1)
The set of all values of λ for which the system of linear equationsÂ
2x1-2x2+x3 = λx1
2x1- 3x2 + 2x3 = λx2
-x1 + 2x2 = λx3
a non- trivial solution.
is an empty set
is a singleton set
contains two elements
contains two elements
If α, β ≠0 and f(n) = αn+ βn and 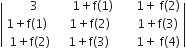
= K(1-α)2(1-β)2(α- β)2, then K is equal toÂ
αβÂ
1/αβÂ
1
1
If A is a 3x3 non- singular matrix such that AAT = ATA, then BBT is equal to
B-1
B-1
Let P and Q be 3 × 3 matrices with P ≠Q. If P3= Q3 and P2Q = Q2P, then determinant of(P2+ Q2) is equal to
-2
1
0
0
The number of values of k for which the linear equations
4x + ky + 2z = 0
kx + 4y + z = 0
2x + 2y + z = 0
posses a non-zero solution is:
3
2
1
1
