Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

51. Represent the following family of curves by forming the corresponding differential equations (a. b: parameters).

straight x squared over straight a squared plus straight y squared over straight b squared space equals space 1

124 Views

52. Represent the following family of curves by forming the corresponding differential equations (a. b: parameters).

straight x squared over straight a squared minus straight y squared over straight b squared space equals space 1

86 Views

53. Represent the following family of curves by forming the corresponding differential equations (a. b: parameters).

straight y squared minus 4 straight a left parenthesis straight x minus straight b right parenthesis

93 Views

54. Represent the following family of curves by forming the corresponding differential equations (a. b: parameters).

left parenthesis straight y minus straight b right parenthesis squared space equals space 4 left parenthesis straight x minus straight a right parenthesis

94 Views

55. Represent the following family of curves by forming the corresponding differential equations (a. b: parameters).

straight x squared plus straight y squared space equals space 2 ax

93 Views

56.

Find the differential equation that will represent the family of curves given by (a, b: parameter):
y = ax³

118 Views

57.

Find the differential equation that will represent the family of curves given by (a, b: parameter):
x² + y² = a x³

97 Views

58.

Find the differential equation that will represent the family of curves given by (a, b: parameter):
y = e^ax

93 Views

The given equation is

straight y squared minus 2 ay plus straight x squared space equals space straight a squared

...(1)
Differentiating both sides w.r.t.x, we get,

2 space straight y space dy over dx minus 2 space straight a dy over dx plus 2 straight x equals 0 space space space or space space straight y dy over dx plus straight x space equals space straight a dy over dx

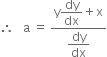therefore space space space straight a space equals space fraction numerator straight y begin display style dy over dx end style plus straight x over denominator begin display style dy over dx end style end fraction

...(2)
Eliminating m from (1) and (2), we get,

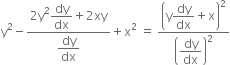
straight y squared minus fraction numerator 2 straight y squared begin display style dy over dx end style plus 2 xy over denominator begin display style dy over dx end style end fraction plus straight x squared space equals space open parentheses straight y begin display style dy over dx end style plus straight x close parentheses squared over open parentheses begin display style dy over dx end style close parentheses squared

open parentheses straight x squared plus straight y squared close parentheses open parentheses dy over dx close parentheses squared minus 2 straight y squared open parentheses dy over dx close parentheses squared minus 2 xy open parentheses dy over dx close parentheses space equals space open parentheses straight y dy over dx plus straight x close parentheses squared

open parentheses straight x squared plus straight y squared close parentheses open parentheses dy over dx close parentheses squared minus 2 straight x squared open parentheses dy over dx close parentheses squared minus 2 xy dy over dx equals straight y squared open parentheses dy over dx close parentheses squared plus straight x squared plus 2 xy dy over dx

open parentheses straight x squared minus 2 straight y squared close parentheses space open parentheses dy over dx close parentheses squared space minus space 4 xy dy over dx minus straight x squared space equals space 0

left parenthesis 2 straight y squared minus straight x squared right parenthesis space open parentheses dy over dx close parentheses squared plus 4 xy dy over dx plus straight x squared space equals space 0

which is required differential equation.

97 Views

60. Form the differential equation representing the family of curves y = a sin (x + b), where a and b are arbitrary constants.

99 Views