Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Differential Equations

Long Answer Type

161.
For the differential equation $xy dy over dx space equals space left parenthesis straight x plus 2 right parenthesis thin space left parenthesis straight y plus 2 right parenthesis comma$ find the solution curve passing through the point (1, -1).

The given differential equation is

straight x space straight y dy over dx space equals space left parenthesis straight x plus 2 right parenthesis thin space left parenthesis straight y plus 2 right parenthesis

Separating the variables, we get,

fraction numerator straight y over denominator straight y plus 2 end fraction dy space equals space fraction numerator straight x plus 2 over denominator straight x end fraction dx

Integrating,

integral fraction numerator straight y over denominator straight y plus 2 end fraction dy space equals space integral fraction numerator straight x plus 2 over denominator straight x end fraction dx

therefore space space space space integral fraction numerator left parenthesis straight y plus 2 right parenthesis space minus space 2 over denominator straight y plus 2 end fraction dy space equals space integral open parentheses straight x over straight x plus 2 over straight x close parentheses dx

therefore space space space space integral open parentheses 1 minus fraction numerator 2 over denominator straight y plus 2 end fraction close parentheses space dy space equals space integral open parentheses 1 plus 2 over straight x close parentheses dx

therefore space space space straight y minus 2 space open vertical bar straight y plus 2 close vertical bar space equals space straight x plus 2 space log open vertical bar straight x close vertical bar space plus space straight c

...(1)
Since the curve passes through (1, -1)

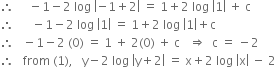
therefore space space space space space minus 1 minus 2 space log space open vertical bar negative 1 plus 2 close vertical bar space equals space 1 plus 2 space log space open vertical bar 1 close vertical bar space plus space straight c therefore space space space space space space minus 1 minus 2 space log space open vertical bar 1 close vertical bar space equals space 1 plus 2 space log space open vertical bar 1 close vertical bar plus straight c therefore space space space minus 1 minus 2 space left parenthesis 0 right parenthesis space equals space 1 space plus space 2 left parenthesis 0 right parenthesis space plus space straight c space space space rightwards double arrow space space straight c space equals space minus 2 therefore space space space from space left parenthesis 1 right parenthesis comma space space space straight y minus 2 space log space open vertical bar straight y plus 2 close vertical bar space equals space straight x plus 2 space log space open vertical bar straight x close vertical bar space minus space 2

straight y minus straight x plus 2 space equals space 2 space log space open vertical bar straight x space left parenthesis straight y plus 2 right parenthesis close vertical bar

straight y minus straight x plus 2 space equals space log space open vertical bar straight x space left parenthesis straight y plus 2 right parenthesis close vertical bar squared

straight y minus straight x plus 2 space equals space log space open square brackets straight x squared space left parenthesis straight y plus 2 right parenthesis squared close square brackets

is the required solution.

81 Views

162. Find the equation of a curve passing through the point (0, – 2) given that at any point (x, y) on the curve, the product of the slope of its tangent and y coordinate of the point is equal to the x coordinate of the point.

89 Views

163. At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (– 4, – 3). Find the equation of the curve given that it passes through ( 2, 1).

79 Views

164. Find the equation of the curve passing through the point

open parentheses 0 comma space straight pi over 4 close parentheses

whose differential equation is sin x cos y dx + cos x sin y dy = 0.

75 Views

165. Find the equation of a curve passing through the point (0, 0) and whose differential equation is y' = e^x sin x.

75 Views

166.

The volume of spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of balloon after t seconds.

102 Views

167. In a bank, principal increases continuously at the rate of 5% per year. In how many years Rs. 1000 double itself ?

88 Views

168. In a bank, principal increases continuously at the rate of r% per year. Find the value of r if Rs. 100 double itself in 10 years.

78 Views

169. In a bank, principal increases continuously at the rate of r% per year. Find the value of r if Rs. 100 double itself in 10 years. (e^0·5 = 1·648).

77 Views

170.

In a culture, the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000, if the rate of growth of bacteria is proportional to the number present?

91 Views

Previous Year Papers

Test Series

Test Yourself

Long Answer Type

161. For the differential equation find the solution curve passing through the point (1, -1).

161.
For the differential equation $xy dy over dx space equals space left parenthesis straight x plus 2 right parenthesis thin space left parenthesis straight y plus 2 right parenthesis comma$ find the solution curve passing through the point (1, -1).