Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Differential Equations

Long Answer Type

171. The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 20.000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009 ?

81 Views

Multiple Choice Questions

172. The general solution of the differential equation

dy over dx space equals space straight e to the power of straight x plus straight y end exponent

e^x + e^{– y} = C
e^x+ e^y = C
e^{– x} + e^y = C
e^{– x} + e^y = C

79 Views

Short Answer Type

173.

Solve $dy over dx space equals space left parenthesis 4 straight x plus straight y plus 1 right parenthesis squared.$

75 Views

Long Answer Type

174.
Solve $left parenthesis straight x minus straight y right parenthesis squared space dy over dx space equals space straight a squared.$

The given differential equation is

left parenthesis straight x minus straight y right parenthesis squared dy over dx space equals space straight a squared

...(1)
Put x - y = t,

therefore space space space space 1 space minus space dy over dx space equals space dt over dx space space or space space dy over dx equals space 1 minus dt over dx

therefore space space space from space left parenthesis 1 right parenthesis comma space space space straight t squared space open parentheses 1 minus dt over dx close parentheses space equals space straight a squared space space space or space space space 1 minus dt over dx space equals space straight a squared over straight t squared

therefore space space space space space space space space space space space space space space space space space minus dt over dx space equals space straight a squared over straight t squared minus 1 space space space space space or space space space space dt over dx space equals space minus fraction numerator straight a squared minus straight t squared over denominator straight t squared end fraction

Separating the variables, we get,

fraction numerator straight t squared over denominator straight a squared minus straight t squared end fraction dt space equals space minus dx

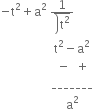
negative straight t squared plus straight a squared space fraction numerator 1 over denominator long division enclose straight t squared end enclose end fraction space space space space space space space space space space space space space space space space space space straight t squared minus straight a squared space space space space space space space space space space space space space space space space space space space minus space space plus space space space space space space space space space space space space space space space space space _______ space space space space space space space space space space space space space space space space space space space space space space straight a squared

Integrating,

integral fraction numerator straight t squared over denominator straight a squared minus straight t squared end fraction dt space equals space minus integral space 1 space dx

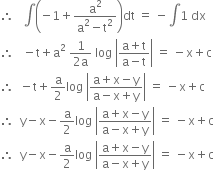
therefore space space space integral open parentheses negative 1 plus fraction numerator straight a squared over denominator straight a squared minus straight t squared end fraction close parentheses dt space equals space minus integral 1 space dx therefore space space space minus straight t plus straight a to the power of 2 space end exponent fraction numerator 1 over denominator 2 straight a end fraction space log space open vertical bar fraction numerator straight a plus straight t over denominator straight a minus straight t end fraction close vertical bar space equals space minus straight x plus straight c therefore space space minus straight t plus straight a over 2 log space open vertical bar fraction numerator straight a plus straight x minus straight y over denominator straight a minus straight x plus straight y end fraction close vertical bar space equals space minus straight x plus straight c therefore space space straight y minus straight x minus straight a over 2 log space open vertical bar fraction numerator straight a plus straight x minus straight y over denominator straight a minus straight x plus straight y end fraction close vertical bar space equals space minus straight x plus straight c therefore space space straight y minus straight x minus straight a over 2 log space open vertical bar fraction numerator straight a plus straight x minus straight y over denominator straight a minus straight x plus straight y end fraction close vertical bar space equals space minus straight x plus straight c

straight y minus straight a over 2 log space open vertical bar fraction numerator straight a plus straight x minus straight y over denominator straight a minus straight x plus straight y end fraction close vertical bar space equals space straight c comma

which is required solution.

75 Views

Short Answer Type

175. Solve the following differential equation:

open parentheses straight x plus straight y close parentheses squared dy over dx space equals straight a squared

75 Views

176. Solve the following differential equation:

open parentheses straight x plus straight y plus 2 close parentheses space dy over dx space equals 2

80 Views

177. Solve the following differential equation:

dy over dx plus 1 space equals space straight e to the power of straight x plus straight y end exponent

75 Views

Long Answer Type

178. Solve the differential equation

dy over dx space equals sin left parenthesis straight x plus straight y right parenthesis space space or space sin to the power of negative 1 end exponent open parentheses dy over dx close parentheses space equals space straight x plus straight y

76 Views

179.

Solve: sin (x+y) $dy over dx space equals 1$ .

79 Views

180.

Solve:
$dy over dx space equals space cos space left parenthesis straight x plus straight y right parenthesis space space or space space cos to the power of negative 1 end exponent open parentheses dy over dx close parentheses space equals space straight x plus straight y$