Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Probability

Short Answer Type

941. State which of the following are not the probability distribution of a random variable. Give reasons for your answer.

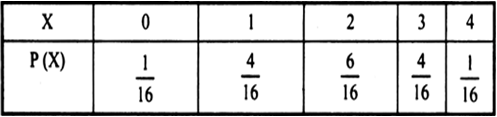
X	0	1	2
P(X)	0.4	0.4	0.2

88 Views

942. State which of the following are not the probability distribution of a random variable. Give reasons for your answer.

X	0	1	2	3	4
P(X)	0.1	0.5	0.2	-0.1	0.3

98 Views

943. State which of the following are not the probability distribution of a random variable. Give reasons for your answer.

Y	-1	0	1
P(Y)	0.6	0.1	0.2

82 Views

944. State which of the following are not the probability distribution of a random variable. Give reasons for your answer.

Z	3	2	1	0	-1
P(Z)	0.3	0.2	0.4	0.1	0.05

89 Views

Long Answer Type

945. Let X denote the number of hours you study during a randomly selected school day. The probability that X can take the value x, has the following form, where k is some unknown constant.

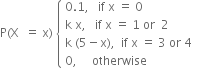
straight P left parenthesis straight X space space equals space straight x right parenthesis space open curly brackets table attributes columnalign left end attributes row cell 0.1 comma space space space if space straight x space equals space 0 end cell row cell straight k space straight x comma space space space if space straight x space equals space 1 space or space space 2 end cell row cell straight k space left parenthesis 5 minus straight x right parenthesis comma space space if space straight x space equals space 3 space or space 4 end cell row cell 0 comma space space space space space otherwise end cell end table close

(a) Find the value of k.
(b). What is the probability that you study at least two hours ? Exactly two hours ? At most two hours?

104 Views

946. A random variable X has the following probability distribution:

X	0	1	2	3	4	5	6	1
P(X)	0	k	2k	2k	3k	k²	2k²	7k² + k

Determine (i) k (ii) P(X < 3) (iii) P(X > 6) (iv) P(0 < X < 3)

137 Views

Short Answer Type

947. The random variable X has probability distribution P(X) of the following rm, where k is some number:

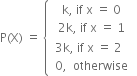
straight P left parenthesis straight X right parenthesis space equals space open curly brackets table row cell straight k comma space if space straight x space equals space 0 end cell row cell 2 straight k comma space if space straight x space equals space 1 end cell row cell table attributes columnalign left end attributes row cell 3 straight k comma space if space straight x space equals space 2 end cell row cell 0 comma space space otherwise end cell end table end cell end table close

(a) Determine the value of k.
(b) Find P(X < 2), P(X ≤ 2), P(X ≥ 2).

84 Views

948. A die (fair) is tossed once. If the random variable is “getting an even number” (denoted by Y), find the probability distribution of Y.

104 Views

949. An unbiased coin is thrown thrice. If the random variable X denotes the number of heads obtained, describe the probability distribution of X.
Or
A coin is tossed three times. Getting a H “head” is a success. If x denotes the number of successes, find the probability distribution of x.

78 Views

Long Answer Type

950. A coin is tossed 4 times. X is the number of heads observed. Find the probability distribution of X.

Here X denotes the number of heads obtained in three tosses of a coin. X can take the values 0, 1, 2, 3, 4.
Let p be the probability of getting a head and q be the probability of not getting a head.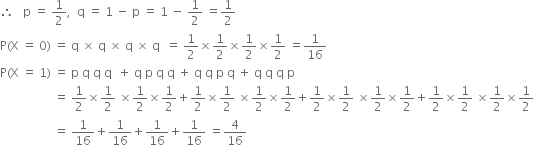
$therefore space space space straight p space equals space 1 half comma space space straight q space equals space 1 space minus space straight p space equals space 1 space minus space 1 half space equals 1 half straight P left parenthesis straight X space equals space 0 right parenthesis space equals space straight q space cross times space straight q space cross times space straight q space cross times space straight q space space equals space 1 half cross times 1 half cross times 1 half cross times 1 half space equals 1 over 16 straight P left parenthesis straight X space equals space 1 right parenthesis space equals space straight p space straight q space straight q space straight q space space plus space straight q space straight p space straight q space straight q space plus space straight q space straight q space straight p space straight q space plus space straight q space straight q space straight q space straight p space space space space space space space space space space space space space space space space space space equals space 1 half cross times 1 half space cross times 1 half cross times 1 half plus 1 half cross times 1 half space cross times 1 half cross times 1 half plus 1 half cross times 1 half space cross times 1 half cross times 1 half plus 1 half cross times 1 half space cross times 1 half cross times 1 half space space space space space space space space space space space space space space space space space space equals space 1 over 16 plus 1 over 16 plus 1 over 16 plus 1 over 16 space equals 4 over 16$
P(X = 2) = p p q q + p q p q + q p p q + p q q p + q p q p + q q p p

$equals space 1 half cross times 1 half cross times 1 half cross times 1 half plus 1 half cross times 1 half cross times 1 half cross times 1 half plus 1 half cross times 1 half cross times 1 half cross times 1 half plus 1 half cross times 1 half cross times 1 half cross times 1 half$

$plus 1 half cross times 1 half cross times 1 half cross times 1 half plus 1 half cross times 1 half cross times 1 half cross times 1 half space equals 6 over 16$
P(X = 3) = p p p q + p p q p + p q p p + q p p p
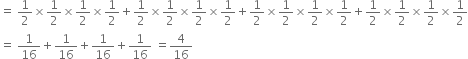
$equals space 1 half cross times 1 half cross times 1 half cross times 1 half plus 1 half cross times 1 half cross times 1 half cross times 1 half plus 1 half cross times 1 half cross times 1 half cross times 1 half plus 1 half cross times 1 half cross times 1 half cross times 1 half equals space 1 over 16 plus 1 over 16 plus 1 over 16 plus 1 over 16 space equals 4 over 16$

P(X = 4) = p p p p = $1 half cross times 1 half cross times 1 half cross times 1 half space equals space 1 over 16$
∴ probability distribution of X is

108 Views