Long Answer Type
are co-planar, find their common point and the equation of the plane in which way they lie. 
...(1)
...(2)
...(3)
we get
or – 1 = – 1 = – 1, which is true
∴ the lines intersect, and ∴ are coplanar
The point of intersection of lines is (–4 + 5, –4 + 7, 5 – 3) i.e. (1,3,2)
The equation of plane in which given lines lie is
or 
or (x – 5) (12+ 5)–(y–7) (12 + 25) + (z + 3) (4 – 28) = 0
or 17 (x – 5) – 47 (y – 7) – 24 (z + 3) = 0
or 17x – 47 y – 24 z + 172 = 0
which is required equation of plane.
Short Answer TypeFind the coordinates of the foot of perpendicular drawn from the point A
(-1,8,4) to the line joining the points B(0,-1,3) and C(2,-3,-1). Hence find the image of the point A in the line BC.
Long Answer TypeFind the equation of the plane which contains the line of intersection of the planes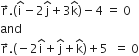
and whose intercept on the x-axis is equal to that of on y-axis.
Short Answer TypeFind x such that the four points A(4, 1, 2), B(5, x, 6) , C(5, 1, -1) and D(7, 4, 0) are coplanar.
A line passing through the point A with position vector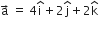 
is parallel to the vector 
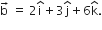Find the length of the perpendicular drawn on this line from a point p with vector 
Switch
on the three axes.
