331.

Find the equation of the plane which contains the line of intersection of the planes 

$\overrightarrow{\mathrm{r}}. \left( \hat{\mathrm{i}} + 2 \hat{\mathrm{j}} + 3 \mathrm{k} \right) - 4 = 0, \overrightarrow{\mathrm{r}}. \left( 2 \hat{\mathrm{i}} + \hat{\mathrm{j}} - \mathrm{k} \right) + 5 = 0$  and which is perpendicular to

the plane  $\overrightarrow{\mathrm{r}}. \left( 5 \hat{\mathrm{i}} + 3 \hat{\mathrm{j}} - 6 \mathrm{k} \right) + 8 = 0$.

If a line has direction ratios 2,-1,-2 then what are its direction cosines?

Find the equation of the line passing through the point  (-1,3,-2)  and

perpendicular to the lines   $\frac{\mathrm{x}}{1} = \frac{\mathrm{y}}{2} = \frac{\mathrm{z}}{3} \mathrm{and} \frac{\mathrm{x} + 2}{- 3} = \frac{\mathrm{y} - 1}{2} = \frac{\mathrm{z} + 1}{5}.$

Find the equation of the plane determined by the point A( 3, - 1, 2 ), B( 5, 2, 4 ) and C( -1, -1, 6 ) and hence find the distance between the plane and the point P( 6, 5, 9 ).

The line passing through  $\left(- 1, \frac{\mathrm{\pi }}{2}\right)$ and perpendicular to 

$\sqrt{3} + \sin \left(\mathrm{\theta }\right) + 2\cos \left(\mathrm{\theta }\right) = \frac{4}{\mathrm{r}} \mathrm{is} :$ 

• $2 = \sqrt{3}\mathrm{rcos}\left(\mathrm{\theta }\right) - 2\mathrm{rsin}\left(\mathrm{\theta }\right)$

• $5 = - 2\sqrt{3}\mathrm{rsin}\left(\mathrm{\theta }\right) + 4\mathrm{rsin}\left(\mathrm{\theta }\right)$

• $2 = \sqrt{3}\mathrm{rcos}\left(\mathrm{\theta }\right) + 2\mathrm{rsin}\left(\mathrm{\theta }\right)$

• $5 = 2\sqrt{3}\mathrm{rsin}\left(\mathrm{\theta }\right) + 4\mathrm{rcos}\left(\mathrm{\theta }\right)$

$$\begin{gathered} \mathrm{If} {\mathrm{m}}_1 \mathrm{and} {\mathrm{m}}_2 \mathrm{are} \mathrm{the} \mathrm{roots} \mathrm{of} \mathrm{the} \mathrm{equation} {\mathrm{x}}^2 + \left(\sqrt{3} + 2\right)\mathrm{x} + \left(\sqrt{3} - 1\right) = 0, \\ \mathrm{then} \mathrm{the} \mathrm{area} \mathrm{of} \mathrm{the} \mathrm{triangle} \mathrm{formed} \mathrm{by} \mathrm{the} \mathrm{lines} \\ \mathrm{y} = {\mathrm{m}}_1\mathrm{x}, \mathrm{y} = {\mathrm{m}}_2\mathrm{x} \mathrm{and} \mathrm{y} = \mathrm{c} \end{gathered}$$

• $\left(\frac{\sqrt{33} - \sqrt{11}}{4}\right){\mathrm{c}}^2$

• $\left(\frac{\sqrt{33} + \sqrt{11}}{4}\right){\mathrm{c}}^2$

• $\left(\frac{\sqrt{11} - \sqrt{33}}{2}\right){\mathrm{c}}^2$

• $\frac{\sqrt{33}}{2}{\mathrm{c}}^2$

 $∆$ABC is formed by A(1, 8, 4), B (0, - 11, 4) and C(2, - 3,1). If D is the foot of the perpendicular from A to BC. Then the coordinates of D are

• ( - 4, 5, 2)

• (4, 5, - 2)

• (4,  - 5, 2)

• (4,  - 5, - 2)

The distance of the point (1, −5, 9) from the plane x−y+z=5 measured along the line x=y=z is:

• 3√10

• 10√3

• 10/√3

• 20/3

If the line  lies in the plane lx +my -z = 9, then l² +m² is equal to 

• 26

• 18

• 5

• 2

Locus the image of the point (2,3) in the line (2x - 3y +4) + k (x-2y+3) = 0, k ε R is a 

• straight line parallel to X - axis

• a straight line parallel to Y- axis

• circle of radius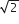 

• circle of radius