The angle between the lines 2x = 3y = − z and 6x = − y = − 4z is

• 0^o

• 90^o

• 45^o

• 45^o

If the plane 2ax − 3ay + 4az + 6 = 0 passes through the midpoint of the line joining the centres of the spheres

x² + y² + z² + 6x − 8y − 2z = 13 and x² + y² + z² − 10x + 4y − 2z = 8, then a equals

• -1

• 1

• -2

• -2

373.

The distance between the line 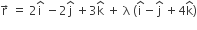 and the plane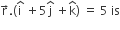 

• 10/9

• 

• 3/10

• 3/10

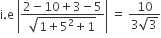
If a vertex of a triangle is (1, 1) and the mid-points of two sides through this vertex are (-1, 2) and (3, 2), then the centroid of the triangle is

• (-1, 7/3)

• (-1/3, 7/3)

• (1, 7/3)

• (1, 7/3)

A and B are two like parallel forces. A couple of moment H lies in the plane of A and B and is contained with them. The resultant of A and B after combining is displaced through a distance

• 2H/A-B

• H/A+B

• H/2(A+B)

• H/2(A+B)

The plane x + 2y – z = 4 cuts the sphere x² + y² + z² – x + z – 2 = 0 in a circle of radius

• 3

• 1

• 2

• 2

Let A (2, –3) and B(–2, 1) be vertices of a triangle ABC. If the centroid of this triangle moves on the line 2x + 3y = 1, then the locus of the vertex C is the line

• 2x + 3y = 9

• 2x – 3y = 7

• 3x + 2y = 5

• 3x + 2y = 5

A line makes the same angle θ, with each of the x and z-axis. If the angle β, which it makes with y-axis, is such that sin²β = 3sin²θ , then cos2θ equals 

• 2/3

• 1/5

• 3/5

• 3/5

Distance between two parallel planes 2x + y + 2z = 8 and 4x + 2y + 4z + 5 = 0 is

• 3/2

• 5/2

• 7/2

• 7/2

A line with direction cosines proportional to 2, 1, 2 meets each of the lines x = y + a = z and x + a = 2y = 2z. The co-ordinates of each of the point of intersection are given by

• (3a, 3a, 3a), (a, a, a)

• (3a, 2a, 3a), (a, a, a)

• (3a, 2a, 3a), (a, a, 2a)

• (3a, 2a, 3a), (a, a, 2a)