Mathematics : Trigonometric Functions

AB is a vertical pole with B at the ground level and A at the top. A man finds that the angle of elevation of the point A from a certain point C on the ground is 60°. He moves away from the pole along the line BC to a point D such that CD = 7 m. From D the angle of elevation of the point A is 45°.
Then the height of the pole is

The value of cot 

• 6/17

• 5/17

• 4/17

• 4/17

• 1

• 3

• 4

• 4

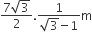
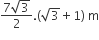
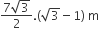
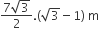
A tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB (= a) subtends an angle of 60º at the foot of the tower, and the angle of elevation of the top of the tower from A or B is 30º. The height of the tower is

The value of 

• i

• 1

• -i

• -i

If 0 < x < π and cosx + sinx = 1/2 , then tanx is

• 
• 

• tan 1

• tan 1

In a triangle PQR, ∠R =π/2. If (P/2) and tan (Q/2) are the roots of ax² +bx+ c = 0, a ≠ 0 then 

• a = b + c

• c = a + b

• b = c

• b = c

In a triangle, ABC, let ∠C = π/2 . If r is the in radius and R is the circumradius of the triangle ABC, then 2 (r + R) equals

• b + c

• a+b

• a + b + c

• a + b + c

• I₂ > I₁

• I₁ > I₂

• I₃ = I₄

• I₃ = I₄