Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Vector Algebra

Short Answer Type

111. Show that the three points A (1, –2, –8) , B (5. 0. –2) and C (11, 3. 7) are collinear and find the ratio in which B divides AC.

108 Views

112. If Q is the point of intersection of the medians of the triangle ABC, then prove that

QA with rightwards arrow on top space plus space QB with rightwards arrow on top space plus space QC with rightwards arrow on top space equals space 0 with rightwards arrow on top.

91 Views

113. ABCD is a parallelogram. E, F are mid-points of BC, CD respectively. AE, AF meet the diaginal BD at Q, P respectively. Show that PQ trisects DB.

Take A as origin. Let

straight b with rightwards arrow on top comma space straight c with rightwards arrow on top comma space straight d with rightwards arrow on top

be the position vectors of B, C, D respectively. Let M be the point of intersection of diagonals of AC and BD.
In ∆ADC, P is the centroid as it is the point of intersection of two medians AF and DM as M is midpoint of AC.

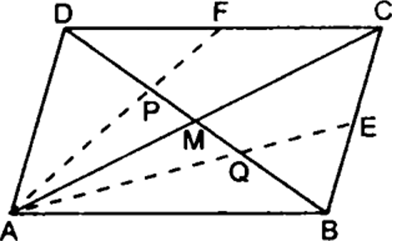
therefore space space space AP with rightwards arrow on top space equals space fraction numerator 0 with rightwards arrow on top space plus space straight d with rightwards arrow on top space plus space straight c with rightwards arrow on top over denominator 3 end fraction space equals space fraction numerator 2 space straight d with rightwards arrow on top space plus straight b with rightwards arrow on top over denominator 3 end fraction

∴ P divides BD in the ratio 2 : 1
Similarly Q divides DB in the ratio 2 : 1
Hence the result.

89 Views

114. If

straight a with rightwards arrow on top comma space straight b with rightwards arrow on top comma space stack straight c comma with rightwards arrow on top straight d with rightwards arrow on top

are any four vectors in 3 - dimensional space with the same initial point and such that

3 space straight a with rightwards arrow on top space space minus space 2 space straight b with rightwards arrow on top space plus space straight c with rightwards arrow on top space minus space 2 space straight d with rightwards arrow on top space equals space 0 with rightwards arrow on top comma space

show that terminals, A, B, C, D of these vectors are coplanar. Find the point at which AC and BD meet. Find the ratio in which P divides AC and BD.

86 Views

115. Four points A, B, C, D with position vectors

straight a with rightwards arrow on top comma space straight b with rightwards arrow on top comma space straight c with rightwards arrow on top comma space straight d with rightwards arrow on top

respectively are such that

3 straight a with rightwards arrow on top space minus space straight b with rightwards arrow on top space plus space space 2 straight c with rightwards arrow on top space minus space 4 space straight d with rightwards arrow on top space equals space 0 with rightwards arrow on top

. Show that the four points are coplanar. Also, find the position vector of the point of intersection of lines AC and BD.

91 Views

Long Answer Type

116. The mid-points of two opposite sides of a quadrilateral and the mid-points of the diagonals are the vertices of a parallelogram. Prove using vectors.

89 Views

Short Answer Type

117. A point P divides a line segment AB in the ratio A : 1. Give the values of A for which
P lies in between AB and
(i) nearer A than B (ii) nearer B than A

82 Views

118. A point P divides a line segment AB in the ratio A : 1. Give the values of A for which P lies outside AB and
(i) nearer A than B (ii) nearer B than A.

78 Views

Long Answer Type

119. Show that the lines joining the mid-points of the opposite sides of a quadrilateral bisect each other.

97 Views

120. Show that a quadrilateral is a parallelogram if an only if diagonals bisect each other.

90 Views