If a = $\hat{\mathrm{i}} + \hat{\mathrm{j}} - 2\hat{\mathrm{k}}, \mathrm{b} = 2\hat{\mathrm{i}} - \hat{\mathrm{j}} + \hat{\mathrm{k}}$ and c = $3\hat{\mathrm{i}} - \hat{\mathrm{k}}$ and c = ma + nb, then m + n is equal to

• 0

• 1

• 2

• - 1

M and N are the mid-points of the diagonals AC and BO respectively of quadrilateral ABCD, then AB + AD + CB + CD is equal to

• 2MN

• 2NM

• 4MN

• 4NM

If $\mathrm{a} = \hat{\mathrm{i}} + \hat{\mathrm{j}} + \hat{\mathrm{k}}$, $\mathrm{b} = 2\hat{\mathrm{i}} + \mathrm{\lambda }\hat{\mathrm{j}} + \hat{\mathrm{k}}$, $\mathrm{c} = \hat{\mathrm{i}} - \hat{\mathrm{j}} + 4\hat{\mathrm{k}}$ and $\mathrm{a} . \left(\mathrm{b} \times \mathrm{c}\right)$ = 10, then $\mathrm{\lambda }$ is equal to

• 6

• 7

• 9

• 10

Let $\square$PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS + QR =

• 3 MN

• 4 MN

• 2 MN

• 2 NM

If vector r with dc's l, m, n is equally inclined to the coordinate axes, then the total number of such vectors is

• 4

• 6

• 8

• 2

If a, b, c are three vectors such that [a b c] = 5, then the value of [a x b, b x c, c x a] is

• 15

• 25

• 20

• 10

557.

Three forces each of magnitude F are applied along the edges of a regular hexagon as shown in the figure. Each side of hexagon is a. What is the resultant moment (torque) of these three forces about centre O ?

• $\frac{3\sqrt{3}}{2}\mathrm{aF}$

• $\frac{1}{2}\mathrm{aF}$

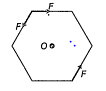
• 3aF

• $\frac{\sqrt{3}}{2}\mathrm{aF}$

The coordinates of a moving point particle in a plane at time t is given by x = a(t + sin(t)), y = a(1 - cos(t)). The magnitude of acceleration of the particle is acceleration ofthe particle is

• 2a

• $\frac{\sqrt{3}}{2}\mathrm{a}$

• a

• $\sqrt{3}\mathrm{a}$

Two vectors A = 3 and B = 4 are perpendicular. Resultant of both these vectors is R. The projection of the vector B on the vector R is

• 5

• 1.25

• 3.2

• 2.4

A vector R is given by R = A x (B x C), which of the following is true ?

• R must be perpendicular to 8

• R is parallel to A

• R must be parallel to B

• None of these