 Multiple Choice Questions
Multiple Choice QuestionsA complex number z is said to be unimodular, if |z|= 1. suppose z1 and z2 are complex numbers such that 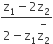 is unimodular and z2 is not unimodular. Then, the point z1 lies on a
is unimodular and z2 is not unimodular. Then, the point z1 lies on a
straight line parallel to X -axis
straight line parallel to Y -axis
circle of radius 2
circle of radius 2
6
-6
3
3
The normal to the curve x2 + 2xy-3y2 =0 at (1,1)
does not meet the curve again
meets the curve again in the second quadrant
meets the curve again in the third quadrant
meets the curve again in the third quadrant
If z is a complex number such that |z|≥2, then the minimum value of 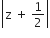
is equal to 5/2
lies in the interval (1,2)
is strictly greater than 5/2
is strictly greater than 5/2
Let α and β be the roots of equation px2 +qx r =0 p ≠0. If p,q and r are in AP and 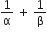 = 4, then the value of |α- β| is
= 4, then the value of |α- β| is




If the coefficients of x3 and x4 in the expansion of (1+ax+bx2)(1-2x)18 in powers of x are both zero, then (a,b) is equal to
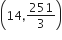
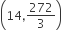
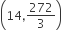
The real number k for which the equation, 2x3 +3x +k = 0 has two distinct real roots in [0,1]
lies between 1 and 2
lies between 2 and 3
lies between -1 and 0
lies between -1 and 0
If the equations x2 + 2x + 3 = 0 and ax2 + bx + c = 0, a, b, c ∈ R, have a common root, then a : b : c is
1:2:3
3:2:1
1:3:2
1:3:2
