Multiple Choice QuestionsThe distance of the point (1, −5, 9) from the plane x−y+z=5 measured along the line x=y=z is:
3√10
10√3
10/√3
20/3
Locus the image of the point (2,3) in the line (2x - 3y +4) + k (x-2y+3) = 0, k ε R is a
straight line parallel to X - axis
a straight line parallel to Y- axis
circle of radius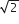 
circle of radius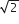
The distance of the point (1,0,2) from the point of intersection of the line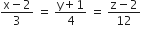 
and the plane x-y +z = 16 is
8
The equation of the plane containing the line 2x-5y +z = 3, x +y+4z = 5 and parallel to the plane x +3y +6z =1 is
2x + 6y + 12z = 13
x+3y+6z = -7
x+3y +6z = 7
x+3y +6z = 7
Distance between two parallel planes 2x + y + 2z = 8 and 4x + 2y + 4z + 5 = 0 is
3/2
5/2
7/2
7/2
If the lines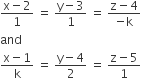
are coplanar, then k can have
any value
exactly one value
exactly two values
exactly two values
If the angle between the line x =
and the plane x + 2y + 3z = 4 is cos-1 
then λ equal
2/3
3/2
2/5
2/5
Statement-1 : The point A(1, 0, 7) is the mirror image of the point B(1, 6, 3) in the line: 
Statement-2: The line:
bisects the line segment joining A(1, 0, 7) and B(1, 6, 3).
Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
Statement-1 is true, Statement-2 is false.
Statement-1 is true, Statement-2 is false.
A line AB in three-dimensional space makes angles 45° and 120° with the positive x-axis and the positive y-axis respectively. If AB makes an acute angle θ with the positive z-axis, then θ
30°
45°
60°
60°
lies in the plane lx +my -z = 9, then l2 +m2 is equal to 
