 Multiple Choice Questions
Multiple Choice QuestionsLet, a, b and c be three non-zero vectors such that no two of them are collinear and 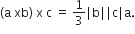 if θ is the angle between vectors b and c, then a value of sin θ is
if θ is the angle between vectors b and c, then a value of sin θ is
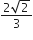
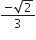
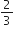
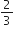
If the vectors AB = 3î + 4k̂ and AC = 5î - 2ĵ + 4k̂ are the sides of a Δ ABC, then the length of the median through A is
√18
√72
√33
√45
Let  be two unit vectors. If the vectors
be two unit vectors. If the vectors 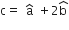 and
and  are perpendicular to each other, then the angle between
are perpendicular to each other, then the angle between  is
is
π/6
π/2
π/3
π/3
Let ABCD be a parallelogram such that  and ∠BAD be an acute angle. If
and ∠BAD be an acute angle. If  is the vector that coincides with the altitude directed from the vertex B the side AD, then
is the vector that coincides with the altitude directed from the vertex B the side AD, then  is given byLet ABCD be a parallelogram such that AB = q,AD = p and ∠BAD be an acute angle. If r is the vector that coincides with the altitude directed from the vertex B to the side AD, then r is given by (1)
is given byLet ABCD be a parallelogram such that AB = q,AD = p and ∠BAD be an acute angle. If r is the vector that coincides with the altitude directed from the vertex B to the side AD, then r is given by (1)
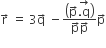
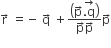
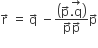
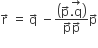
The vector  are not perpendicular and
are not perpendicular and  are two vectors satisfying:
are two vectors satisfying:  The vector
The vector  is equal to
is equal to

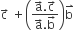
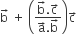
The circle x2+ y2 = 4x + 8y + 5 intersects the line 3x – 4y = m at two distinct points if
-85 < m < -35
-35 < m < 15
15 < m < 65
15 < m < 65
If the vectors 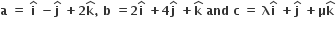 are mutually orthogonal, then (λ,μ) is equal to
are mutually orthogonal, then (λ,μ) is equal to
(-3,2)
(2,-3)
(-2,3)
(-2,3)
A.
(-3,2)
since, the given vectors mutually orthogonal, therefore
a.b = 2-4+2 = 0
a.c = λ-1 + 2μ = 0 ....(i)
b.c = 2λ + 4 +μ = 0 ... (ii)
On solving Eqs. (i) and (ii), we get
μ = 2 and λ = - 3
Hence, (λ,μ) = (-3,2)
