 Multiple Choice Questions
Multiple Choice QuestionsFrom a solid sphere of mass M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendicular to one of its faces is :
h2/4R
3h/4
5h/8
3h2/8R
From a solid sphere of mass M and radius R, a cube of the maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendicular to one of its faces is
![]()
![]()
![]()
![]()
A bob of mass m attached to an inextensible string of length l is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω rad/s about the vertical. About the point of suspension
angular momentum is conserved
angular momentum changes in magnitude but not in the direction
angular momentum changes in direction but not in magnitude
angular momentum changes in direction but not in magnitude
A metallic rod of length ‘l’ is tied to a string of length 2l and made to rotate with angular speed ω on a horizontal table with one end of the string fixed. If there is a vertical magnetic field ‘B’ in the region, the e.m.f. induced across the ends of the rod is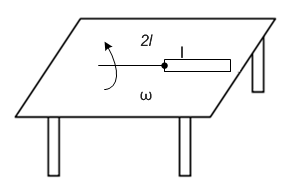
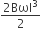
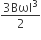
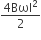
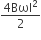
This question has Statement I and Statement II. Of the four choices given after the Statements, choose the
one that best describes the two Statements.
Statement – I: A point particle of mass m moving with speed v collides with stationary point particle of mass M. If the maximum energy loss possible is given as f 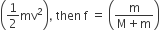
Statement – II : Maximum energy loss occurs when the particles get stuck together as a result of the collision.
Statement – I is true, Statement – II is true, Statement – II is a correct explanation of Statement – I.
Statement – I is true, Statement – II is true, Statement – II is not a correct explanation of Statement – I.
Statement – I is true, Statement – II is false.
Statement – I is true, Statement – II is false.
A hoop of radius r and mass m rotating with an angular velocity ω0
is placed on a rough horizontal surface.The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?
rω0/4
rω0/3
rω0/2
rω0/2
A diatomic molecule is made of two masses m1 and m2 which are separated by a distance r. If we calculate its rotational energy by applying Bohr's rule of angular momentum quantization, its energy will be given by (n is an integer)
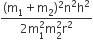
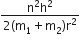
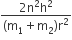
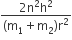
A cylindrical tube, open at both ends, has a fundamental frequency, f, in the air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air-column is now
m1r1:m2r2
m1 :m2
r1 :r2
r1 :r2
A thin horizontal circular disc is rotating about a vertical axis passing through its centre. An insect is at rest at a point near the rim of the disc. The insect now moves along a diameter of the disc to reach its other end. During the journey of the insect, the angular speed of the disc
remains unchanged
continuously decreases
continuously increases
continuously increases
Two identical charged spheres suspended from a common point by two massless strings of length l are initially a distance d(d < < l) apart because of their mutual repulsion. The charge begins to leak from both the spheres at a constant rate.As a result the charges approach each other with a velocity v. Then as a function of distance x between them
v ∝ x-1
v ∝ x1/2
v ∝ x
v ∝ x
