 Multiple Choice Questions
Multiple Choice QuestionsWhat would be the equation of the line, which intercepts x-axis at -5 and perpendicular to the line y = 2x - 3?
x - 2y = -5
x + 2y = 5
x + 2y = -5
x - 2y = 5
The area of the triangle formed by the graphs of the equations x = 4, y = 3 and 3x + 4y = 12 is
4 sq units
12 sq units
6 sq units
6 sq units
The coordinates of the vertices of a right angled triangle are P(3, 4), Q(7, 4) and R(3, 8), the right angle being at P. The coordinates of the orthocentre of ![]() are
are
(3, 4)
(7, 4)
(3, 8)
(3, 8)
The area (in square units) of the triangle formed by the graphs of the equations x = 4, y = 3 and 3x + 4y = 12 is
24
12
6
6
If the ordinate and abscissa of the point (k, 2k -1) be equal, then the value of k is
0
-1
1
1
Area of the triangle formed by the graph of the straight lines x - y = 0, x + y = 2 and x-axis is
1 sq unit
2 sq units
1 sq units
None of these
The graphs of x + 2y = 3 and 3x - 2y = 1 meet the Y-axis at two points having distance

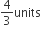
1 unit
1 unit
The value of k for which the graphs of (k - 1)x + y - 2 = 0 and (2 - k)x - 3y + 1 = 0 are parallel is
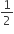
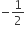
2
2
The area of the triangle formed by the straight line 3x + 2y = 6 and the co-ordinate axes is
3 square units
6 square units
4 square units
4 square units
The length of the intercept of the graph of the equation 9x - 12y = 108 between the two axes is
15 units
9 units
12 units
18 units
