Which one of the following is most essential in learning mathematics at upper primary level?

• Exploring different ways of solving a problem.
  
  

• Memorising all formulas.
  
  

• Copying correctly what teacher writes on the board.
  
  

• Solving a problem many times.

The strategy of questioning used in the mathematics class at upper primary level

• makes the classroom noisy as the children would be taking too much
  
  

• could create stress among children and may lead them to accept the teacher's authority
  
  

• helps children to express their thoughts or understanding and think critically
  
  

• should be discouraged as it demoralises the child who is unable to answer 

While teaching 'shapes', a teacher can plan a trip to historical places, as
A. it needs to provide leisure time as most of the syllabus has been completed in time.
B. it would be an opportunity to improve communication skill.
C. shapes are an integral part of every architecture and such trips encourage connections across disciplines.
D. Field trips are recommended by Education Board, so must be organised.
Select the correct answer using the codes given below.

• C
  
  

• A, C and D
  
  

• B and C
  
  

• A and B

Which among the following is the best pedagogical way to teach Mathematics?

• Motivate the learners to develop their existing capabilities
  
  

• Find the weakness and teach only those parts
  
  

• Find the gaps and address only them
  
  

• Teach every students with the same approach

Ameena is playing with matchsticks and adds one at each stage

Appu, on the other hand, makes a table 

What is your observation about the two children in this situation?

• Ameena will need lots of matchsticks to come to a generalisation. However, Appu would be faster.

• Both Ameena and Appu are trying to make generalisations

• Ameena would be learning by doing and Appu may not be able to see the pattern at all.

• Ameena is only playing and Appu is doing Mathematics.

To be good in Mathematics, one needs to

• have mastery over calculations
  
  

• create and formulate problems through abstract thinking and logical reasoning
  
  

• memorise formulae
  
  

• remember solutions

When introducing mensuration, a teacher writes all the formulae on the board before proceeding further. This reflects that she is following the

• deductive approach
  
  

• experimental approach
  
  

• practical approach
  
  

• inductive approach

Teachers, while discussing problem-solving as an approach to teaching of Mathematics, articulated four views. Which of the following views does not justify the real meaning of this approach?

• 'I think many questions found in the Mathematics textbook can be used for problem-solving.'
  
  

• 'I think it is better to connect problem-solving with general Mathematics class.'
  
  

• 'I think there is no correlation between problem-solving and mathematical reasoning.'
  
  

• 'I think questions on problem- solving should be made from situations based on real-life.'

A cyclist at 'C' is cycling towards 'B'. How far will he have to cycle from C before he is equidistant from both A and B?

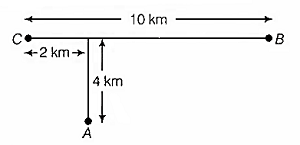
• 3 km
  
  

• 6 km
  
  

• 5 km
  
  

• 4 km

A student observed the following examples
(10)²
= (5+5)² = 5² + 2(5)(5) + (5)² = 100
= (6+4)² = 6² + 2(6)(4) + (4)² = 100
= (8+2)² = 8² + 2(8)(2) + (2)² = 100
= (1+9)² = 1² + 2(1)(9) + (9)² = 100

and concluded that

(a +b)² =a²+2(a)(b) + b²

The above method of drawing conclusions is

• analytical

• activity

• deductive

• inductive