 Multiple Choice Questions
Multiple Choice QuestionsAn ellipse is drawn by taking a diameter of the circle (x–1)2 + y2 = 1 as its semiminor axis and a diameter of the circle x2 + (y – 2)2 = 4 as its semi-major axis. If the centre of the ellipse is the origin and its axes are the coordinate axes, then the equation of the ellipse is
4x2+ y2 = 4
x2 +4y2 =8
4x2 +y2 =8
4x2 +y2 =8
For a regular polygon, let r and R be the radii of the inscribed and the circumscribed circles. A false statement among the following is
there is a regular polygon with r/R = 1/2
there is a regular polygon with 
there is a regular polygon with r/R = 2/3
there is a regular polygon with r/R = 2/3
hyperbola passes through the point P(√2, √3) and has foci at (± 2, 0). Then the tangent to this hyperbola at P also passes through the point
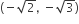
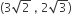
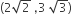
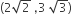
The eccentricity of an ellipse whose centre is at the origin is 1/2. If one of its directives is x= –4, then the equation of the normal to it at (1,3/2) is
x + 2y = 4
2y – x = 2
4x – 2y = 1
4x – 2y = 1
The ellipse x2+ 4y2= 4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is
x2+ 16y2= 16
x2+ 12y2= 16
4x2+ 48y2= 48
4x2+ 48y2= 48
A focus of an ellipse is at the origin. The directrix is the line x = 4 and the eccentricity is 1/2. Then the length of the semi−major axis is
8/3
2/3
5/3
5/3
A parabola has the origin as its focus and the line x = 2 as the directrix. Then the vertex of the parabola is at
(0, 2)
(1, 0)
(0,1)
(0,1)
Consider a family of circles which are passing through the point (-1, 1) and are tangent to x-axis. If (h, K) are the co-ordinates of the centre of the circles, then the set of values of k is given by the interva
0 < k < 1/2
k ≥ 1/2
– 1/2 ≤ k ≤ 1/2
– 1/2 ≤ k ≤ 1/2
The differential equation of all circles passing through the origin and having their centres on the x-axis is
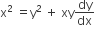
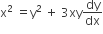
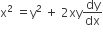
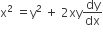
The normal to a curve at P(x, y) meets the x-axis at G. If the distance of G from the origin is twice the abscissa of P, then the curve is a
ellipse
parabola
circle
circle
