 Multiple Choice Questions
Multiple Choice QuestionsThe number of integers greater than 6000 that can be formed, using the digits 3,5,6,7 and 8 without repetition, is
216
192
120
120
If m is the AMN of two distinct real numbers l and n (l,n>1) and G1, G2, and G3 are three geometric means between l and n, then 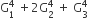 equals
equals
4l2 mn
4lm2n
4 lmn2
4 lmn2
B.
4lm2n
Given,
m is the AM of l and n
l +n = 2m
and G1, G2, G3, n are in GP
Let r be the common ratio of this GP
G1 = lr
G2 =lr2
G3= lr3
n = lr4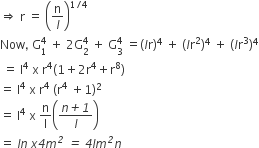
How many different words can be formed by jumbling the letters in the word MISSISSIPPI in which no two S are adjacent?
8 . 6C4 . 7C4
6 . 7 . 8C4
6 . 8 . 7C4
6 . 8 . 7C4
The set S: {1, 2, 3, …, 12} is to be partitioned into three sets A, B, C of equal size. Thus, A ∪ B ∪ C = S, A ∩ B = B ∩ C = A ∩ C = φ. The number of ways to partition S is-
12!/3!(4!)3
12!/3!(3!)4
12!/(4!)3
12!/(4!)3
How many ways are there to arrange the letters in the word GARDEN with the vowels in alphabetical order?
120
480
360
360
The number of ways of distributing 8 identical balls in 3 distinct boxes so that none of the boxes is empty is
5
38
38
The greatest integer which divides (p + 1) (p + 2) (p + 3) .... (p + q) for all p E N and fixed q N is
p!
q!
p
q
The number of ways in which the letters of the word ARRANGE can be permuted such that the R's occur together, is
