 Multiple Choice Questions
Multiple Choice QuestionsConsider 5 independent Bernoulliís trials each with a probability of success p. If the probability of at least one failure is greater than or equal to 31/32, then p lies in the interval
(1/2, 3/4]
(3/4, 11/12]
[0, 1/2]
[0, 1/2]
If two different numbers are taken from the set {0, 1, 2, 3, ......., 10), then the probability that their sum, as well as absolute difference, are both multiple of 4, is
7/55
6/55
14/55
14/55
For three events A, B and C,
P(Exactly one of A or B occurs)
= P(Exactly one of B or C occurs)
= P(Exactly one of C or A occurs) = 1/4and P(All the three events occur simultaneously) = 1/16.Then the probability that at least one of the events occurs, is
3/16
7/32
7/16
7/16
C.
7/16
P(exactly one of A or B occurs)
= P(A) + P(B) – 2P(A ∩ B) =1/4
P(Exactly one of B or C occurs)
= P(B) + P(C) – 2P(B ∩ C) =1/4
P(Exactly one of C or A occurs)
= P(C) + P(A) – 2P(C ∩ A) =1/4
Adding all, we get
2ΣP(A) – 2ΣP(A ∩ B) =3/4
∴ΣP(A) – ΣP(A ∩ B) =3/8
Now, P(A ∩ B ∩ C) =1/16
(Given)
∴ P(A ∪ B ∪ C)
= ΣP(A) – ΣP(A∩B) + P(A ∩ B ∩ C)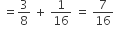
One ticket is selected at random from 50 tickets numbered 00, 01, 02, ... , 49. Then the probability that the sum of the digits on the selected ticket is 8, given that the product of these digits is zero, equals
1/14
1/7
5/14
5/14
The average marks of boys in a class is 52 and that of girls is 42. The average marks of boys and girls combined is 50. The percentage of boys in the class is
40
20
80
80
Suppose a population A has 100 observations 101, 102, … , 200, and another population B has 100 observations 151, 152, … , 250. If VA and VB represent the variances of the two populations, respectively, then VA/VB is
1
9/4
4/9
4/9
At an election, a voter may vote for any number of candidates, not greater than the number to be elected. There are 10 candidates and 4 are of be elected. If a voter votes for at least one candidate, then the number of ways in which he can vote is
5040
6210
385
385
The probability that A speaks truth is 4/ 5 , while this probability for B is 3/ 4 . The probability that they contradict each other when asked to speak on a fact is
3/20
1/20
7/20
7/20
From 6 different novels and 3 different dictionaries, 4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. The number of such arrangements is
At least 750 but less than 1000
At least 1000
Less then 500
At least 500 but less than 750
