 Multiple Choice Questions
Multiple Choice QuestionsIf the function g(x) =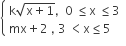 is differntiable, then the value of k+m is
is differntiable, then the value of k+m is
2
16/5
10/3
10/3
A.
2
Since, g(x) is differentiable ⇒ g(x) must be continuous.
therefore, 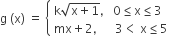
At x =3, RHL = 3m+2
and at x = 3, LHL= 2k
therefore, 2k = 3m + 2 ... (i)
Also, g'(x) = 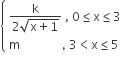
therefore, L{g'(3)} = k/4 and R{g'(3)} = m
⇒ k/4 = m i.e, k = 4m ..... (ii)
On solving eqs (i) and (ii), we get
k = 8/5, m =2/5
⇒ k+m =2
If a ε R and the equation - 3(x-[x]2 + 2(x-[x] +a2 = 0(where,[x] denotes the greatest integer ≤ x) has no integral solution, then all possible value of lie in the interval
(-1,0) ∪ (0,1)
(1,2)
(-2,-1)
(-∞,-2) ∪ (2, ∞)
Consider the following relations:
R = {(x, y)| x, y are real numbers and x = wy for some rational number w}; S = {(m/p, p/q)| m, n, p and q are integers such that n, q ≠ 0 and qm = pn}. Then
R is an equivalence relation but S is not an equivalence relation
neither R nor S is an equivalence relation
S is an equivalence relation but R is not an equivalence relation
S is an equivalence relation but R is not an equivalence relation
Let p(x) be a function defined on R such that 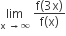 = 1, p'(x) p'(1-x),for all x∈[0,1] p(0) = 1 and p(1) = 41. Then
= 1, p'(x) p'(1-x),for all x∈[0,1] p(0) = 1 and p(1) = 41. Then 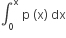 equals
equals
√41
21
41
41
The function 
neither injective nor surjective.
invertible
injective but not surjective.
injective but not surjective.
Let W denote the words in the English dictionary. Define the relation R by :
R = {(x, y) ∈ W × W | the words x and y have at least one letter in common}. Then R is
not reflexive, symmetric and transitive
reflexive, symmetric and not transitive
reflexive, symmetric and transitive
reflexive, symmetric and transitive
The graph of the function y = f(x) is symmetrical about the line x = 2, then
f(x + 2)= f(x – 2)
f(2 + x) = f(2 – x)
f(x) = f(-x)
f(x) = f(-x)
