Two spherical conductors A and B of radii 1 mm and 2 mm are separated by a distance of 5 cm and are uniformly charged. If the spheres are connected by a conducting wire then in equilibrium condition, the ratio of the magnitude of the electric fields at the surface of spheres A and B is

• 1 : 4

• 4 : 1

• 1:2

• 1:2

Which of the following units denotes the dimensions ML² /Q², where Q denotes the electric charge?

• Weber (Wb)

• Henry (H)

• Wb/m²

• Wb/m²

A charged ball B hangs from a silk thread S which makes an angle θ with a large charged conducting sheet P, as shown in the figure. The surface charge density σ of the sheet is proportional to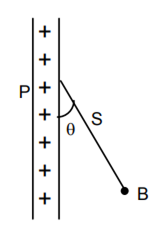

• cos θ

• cot θ

• sin θ

• sin θ

Two point charges + 8q and – 2q are located at x = 0 and x = L respectively. The location of a point on the x axis at which the net electric field due to these two point charges is zero is

• 2L

• L/4

• 8L

• 8L

Two thin wires rings each having a radius R are placed at a distance d apart with their axes coinciding. The charges on the two rings are +q and –q. The potential difference between the centres of the two rings is 

• 
• 

• zero

• zero

A charged particle q is shot towards another charged particle Q which is fixed, with a speed v it approaches Q upto a closest distance r and then returns. If q were given a speed 2v, the closest distances of approach would be

• r

• 2r

• r/2

• r/2

Four charges equal to −Q are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium the value of q is

18.

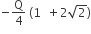
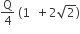
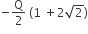
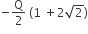
From a uniform circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is:

• $\frac{37}{9}M{R}^2$

• 4MR²

• $\frac{40}{9}M{R}^2$

• 10 MR²

A charge Q placed at the centre of a metallic spherical shell with inner and outer radii R₁ and R₂ respectively. The normal component of the electric field at any point on the Gaussian surface with radius between R₁ and R₂ will be

• Zero

• $\frac{\mathrm{Q}}{4{{\mathrm{\pi R}}_1}^2}$

• $\frac{\mathrm{Q}}{4{{\mathrm{\pi R}}_2}^2}$

• $\frac{\mathrm{Q}}{4\mathrm{\pi } ({\mathrm{R}}_1 - {\mathrm{R}}_2{)}^2}$

A sphere of radius R has a uniform volume charge density ρ. The magnitude of electric field at a distance r from the centre of the sphere, where r > R, is

• $\frac{\mathrm{\rho }}{4{\mathrm{\pi \epsilon }}_0{\mathrm{r}}^2}$

• $\frac{{\mathrm{\rho R}}^2}{{\mathrm{\epsilon }}_0{\mathrm{r}}^2}$

• $\frac{{\mathrm{\rho R}}^3}{{\mathrm{\epsilon }}_0{\mathrm{r}}^2}$

• $\frac{{\mathrm{\rho R}}^3}{3{\mathrm{\epsilon }}_0{\mathrm{r}}^2}$