 Multiple Choice Questions
Multiple Choice QuestionsThe magnetic flux linked with the coil varies with time as . The magnitude of the induced emf at 2 s is
9 V
16 V
3 V
4 V
Two thin metallic strips, carrying current in the direction shown, cross each other perpendicularly without touching but being close to each other, as shown in the figure. The regions which contain some points of zero magnetic induction are
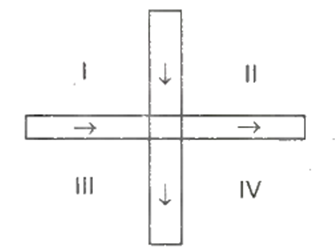
I and II
I and III
I and IV
II and III
The coefficient of mutual inductance between the primary and secondary of the coil is 5 H. A current of 10 A is cut off in 0.5 s. The induced emf is
1 V
10 V
5 V
100 V
Two circuits have mutual inductance of 0.1 H. What average emf is induced in one circuit when the current in the other circuit changes from 0 to 20 A in 0.02 s ?
240 V
230 V
100 V
300 V
The magnetic flux linked with a coil at any instant 't' is given by the emf induced in the coil at t = 2 second is
40 V
− 40 V
300 V
140 V
The induction coil works on the principle of
self-induction
mutual induction
Ampere's rule
Flemmg's right hand rule
The square root of the product of inductance and capacitance has the dimension of
length
mass
time
no dimension
Current in a coil changes from 4 A to zero in 0.1 s and the emf induced is 100 V. The self inductance of the coil is
0.25 H
0.4 H
2.5 H
4 H
The energy stored in an inductor of self inductance L henry carrying a current of I ampere is
LI2
L2I
