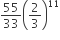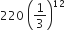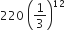Probability

Four numbers are chosen at random from{1, 2, 3, ..., 40}. The probability that they are not consecutive, is

• $\frac{1}{2470}$

• $\frac{4}{7969}$

• $\frac{2469}{2470}$

• $\frac{7965}{7969}$

If A and B are mutually exclusive events with P(B) $\ne$ 1, then P(A$|$$\overline{\mathrm{B}}$) is equal to(Here is the complement of the event B)

• $\frac{1}{\mathrm{P}\left(\mathrm{B}\right)}$

• $\frac{1}{1 - \mathrm{P}\left(\mathrm{B}\right)}$

• $\frac{\mathrm{P}\left(\mathrm{A}\right)}{\mathrm{P}\left(\mathrm{B}\right)}$

• $\frac{\mathrm{P}\left(\mathrm{A}\right)}{1 - \mathrm{P}\left(\mathrm{B}\right)}$

Seven white balls and three black balls are randomly arranged in a row. The probability that no two black balls are placed adjacently is

• $\frac{1}{2}$

• $\frac{7}{15}$

• $\frac{2}{15}$

• $\frac{1}{3}$

A student has to answer 10 out of 13 questions in an examination choosing atleast 5 questions from the first 6 questions. The number of choice available to the student is

• 63

• 91

• 161

• 196

A candidate takes three tests in succession and the probability of passing the first test is p. The probability of passing each succeeding test is p or $\frac{\mathrm{p}}{2}$ according as he passes or fails in the preceding one. The candidate is selected, if he passes atleast two tests. The probability that the candidate is selected, is

• p²(2 - p)

• p(2 - p)

• p + p² + p³

• p²(1 - p)

Two persons A and B are throwing an unbiased six faced dice alternatively, with the condition that the person who throws 3 first wins the game. If A starts the game, then probabilities of A and B to win the same are, respectively

• $\frac{6}{11}, \frac{5}{11}$

• $\frac{5}{11}, \frac{6}{11}$

• $\frac{8}{11}, \frac{3}{11}$

• $\frac{3}{11}, \frac{8}{11}$

3 out of 6 vertices of a regular hexagon are chosen at a time at random. The probability that the triangle formed with these three vertices is an equilateral triangle, is

• $\frac{1}{2}$

• $\frac{1}{5}$

• $\frac{1}{10}$

• $\frac{1}{20}$

A bag P contains 5 white marbles and 3 black marbles. Four marbles are drawn at random from P and are put in an empty bag Q. If a marble drawn at random from Q is found to be black then the probability that all the three black marbles in P are transfered to the bag Q

• $\frac{1}{7}$

• $\frac{6}{7}$

• $\frac{1}{8}$

• $\frac{7}{8}$

There are 10 intermediate stations on a railway line between two particular stations. The number ofways that a train can be made to stop at 3 of these intermediate stations so that no two of these halting stations are consecutive is

• 56

• 20

• 126

• 120

If 12 identical balls are to be placed in 3 identical boxes, then the probability that  one of the boxes contains exactly 3 balls, is