CBSE
 Multiple Choice Questions
Multiple Choice Questions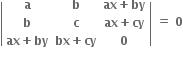 અને ax2 + 2bxy + cy2 ≠ 0 તો.........
અને ax2 + 2bxy + cy2 ≠ 0 તો.........
a, b, cસમગુણોત્તર શ્રેણીમાં છે.
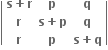 ની કિંમત ....... છે.
ની કિંમત ....... છે.
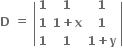 જ્યાં x ≠ 0, y ≠ 0 તો D એ ....... x, y ∈ N
જ્યાં x ≠ 0, y ≠ 0 તો D એ ....... x, y ∈ N
x અને y વડે વિભાજ્ય છે.
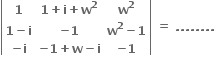
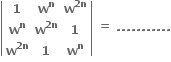
સ્વરિત શ્રેણીમાં
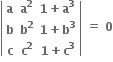 અને સદિશો (1, a, a2) ; (1, b, b2) અને (1, c, c2) એ સમતલીય હોય, તો abc = ......
અને સદિશો (1, a, a2) ; (1, b, b2) અને (1, c, c2) એ સમતલીય હોય, તો abc = ...... A.
-2Tips: -
ધારો કે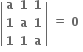
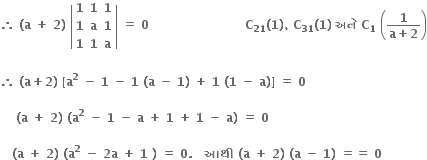
a = -2 લેતાં 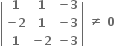 આથી a = -2 માટે x નો છેદ શુન્ય હોવાથી સમીકરણનો એક પણ ઉકેલ નથી.
આથી a = -2 માટે x નો છેદ શુન્ય હોવાથી સમીકરણનો એક પણ ઉકેલ નથી.
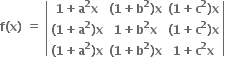 તો, f(x) એ ..........ઘાતવાળી બહુપદી થાય.
તો, f(x) એ ..........ઘાતવાળી બહુપદી થાય.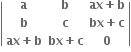 નું મૂલ્ય ......... છે.
નું મૂલ્ય ......... છે.ઋણ