Motion in Straight Line

A monkey of mass 30 kg climbs on a massless rope whose breaking strength is 450 N. The rope will break if the monkey (Take g = 10 m/s² )

• climbs up with a uniform speed of 5 m/s

• climbs down with an acceleration 4 m/s²

• climbs up with an acceleration 6 m/s²

• climbs down with a uniform speed of 5 m/s²

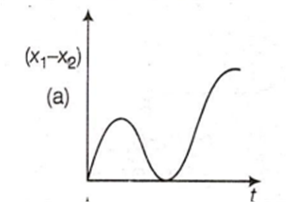
A body is at rest at x = 0 and t = 0, it starts moving in the positive X-direction with a constant acceleration. At the same instant, another body passes through x = O moving in the positive X-direction with a constant speed. The position of the first body is given by x₁ (t) after time t and that of second body by x₂ (t) after the same time interval. Which of the following graphs correctly describes (x_1 − x₂) as a function of time t ?

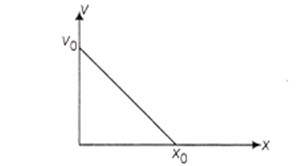
The given graph shows the variation of velocity with displacement. Which one of the graphs given below correctly represents the variation of acceleration with displacement.

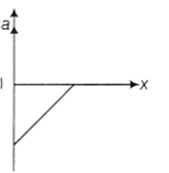
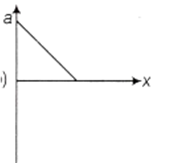
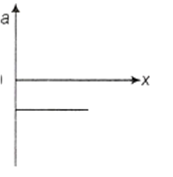
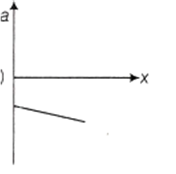
In figure shown below, a particle is travelling counter clockwise in circle of radius 10 m. The acceleration vector indicated at a specific time. Find the value of 'v' at this time.

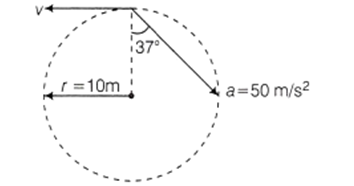
• 10 m/s

• 15 m/s

• 20 m/s

• 7 m/s

A ball which is at rest is dropped from a height h metre.  As it bounces off the floor its speed is 80% of what it was just before touching the ground. The ball will then rise to nearly a height

• 0.94 h

• 0.80 h

• 0.75 h

• 0.64 h

Two bodies of different masses are dropped from heights of 16 m and 25 m respectively. The ratio ofthe time taken by them to reach the ground is

• $\frac{25}{16}$

• $\frac{5}{4}$

• $\frac{4}{5}$

• $\frac{16}{25}$

A man of height h walks in a straight path towards a lamp post of height H with uniform velocity u. Then the velocity of the edge of the shadow on the ground will be

• $\frac{\mathrm{hu}}{\left(\mathrm{H} - \mathrm{h}\right)}$

• $\frac{\mathrm{Hu}}{\left(\mathrm{H} + \mathrm{h}\right)}$

• $\frac{\left(\mathrm{H} - \mathrm{h}\right)}{\mathrm{Hu}}$

• $\frac{\left(\mathrm{H} + \mathrm{h}\right)}{\mathrm{Hu}}$

A train of 150 m length is going towards north direction at a speed of 10 ms^-1 . A parrot flies at a ,speed of 5ms^-1 towards south direction parallel to the railway track. The time taken by the parrot to cross the train is equal to

• 12 s

• 8 s

• 15 s

• 10 s

The area under acceleration-time graph gives

• distance travelled

• change in acceleration

• force acting

• change in velocity

The distance travelled by an object along a straight line in time t is given by s= 3 − 4t + 5t², the initial velocity of the object is

• 3 unit

• − 3 unit 

• 4 unit

• − 4 unit