CBSE Class 10 Mathematics Solved Question Paper 2013

The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30^o. The distance of the car from the base of the tower (in m.) is

• 25√3

• 50√3

• 75√3

• 150

The probability of getting an even number, when a die is thrown once, is

• $\frac{1}{2}$

• $\frac{1}{3}$

• $\frac{1}{6}$

• $\frac{5}{6}$

A box contains 90 discs, numbered from 1 to 90. If one disc is drawn at random from the box, the probability that it bears a prime-number less than 23,is

• $\frac{7}{90}$

• $\frac{10}{90}$

• $\frac{4}{45}$

• $\frac{9}{89}$

If the difference between the circumference and the radius of a circle is 37cm, then using $\mathrm{\pi } = \frac{22}{7}$ , the circumference (in cm) of the circle is:

• 154

• 44

• 14

• 7

The common difference of AP $\frac{1}{3q}. \frac{1-6q}{3q}, \frac{1-12q}{3q}, ........ is;$1 1 6q 1 12q, , 3q 3q 3q
... is:

• q

• -q

• -2

• 2

In fig., a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, $\angle$B = 90^o and DS = 5 cm, then the radius of thecircle (in cm) is 

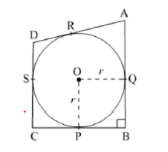
• 11

• 18

• 6

• 15

In fig., PA and PB are two tangents drawn from an external point P to a circlewith centre C and radius 4 cm. If PA PB, then the length of each tangent is

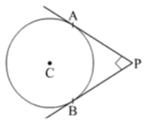
• 3

• 4

• 5

• 6

In fig., the area of triangle ABC (in sq. units) is

• 15

• 10

• 7.5

• 2.5

How many three-digit natural numbers are divisible by 7?

Solve the following quadratic equation for x;$4\sqrt{3}{x}^2 + 5x - 2\sqrt{3} = 0$