If the total surface area of a solid hemisphere is 462 cm², find its volume.

$\left[\mathrm{Take} \mathrm{\pi }= \frac{22}{7}\right]$

12.

Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.

Find the values of k for which the quadratic equation

9x² - 3kx + k = 0 has equal roots.

Solve for x:
   

$\frac{16}{\mathrm{x}} - 1 = \frac{15}{\mathrm{x}+1}; \mathrm{x} \ne 0, -1$

The largest possible sphere is carved out of a wooden solid cube of side 7 cm. Find the volume of the wood left. $\left[Use \pi =\frac{22}{7}\right]$

Water in a canal, 6 m wide and 1.5 m deep, is flowing at a speed of 4 km/h. How much area will it irrigate in 10 minutes, if 8 cm of standing water is needed for irrigation?

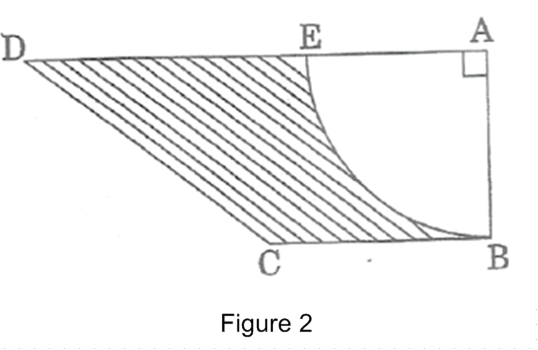
In Figure 2, ABCD is a trapezium of area 24.5 sq. cm. In it, AD|| BC, $\angle$ DAB = $90°$, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region.    $\left[\mathrm{Take} \mathrm{\pi }= \frac{22}{7}\right]$                  

Find the ratio in which the line segment joining the points A(3,- 3) and B(- 2, 7) is divided by x-axis. Also find the coordinates of the point of division

The sum of the 2nd and the 7th terms of an AP is 30. If its 15th term is 1 less than twice its 8th term, find the AP.

Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.